JavaScript-Algorithmen und Datenstrukturen

Dieses Repository enthält JavaScript Beispiele für viele gängige Algorithmen und Datenstrukturen.

Jeder Algorithmus und jede Datenstruktur hat eine eigene README mit zugehörigen Erklärungen und weiterführenden Links (einschließlich zu YouTube-Videos).

Lies dies in anderen Sprachen: English 简体中文, 繁體中文, 한국어, 日本語, Polski, Français, Español, Português, Русский, Türk, Italiana, Bahasa Indonesia, Українська, Arabic, Uzbek

☝ Beachte, dass dieses Projekt nur für Lern- und Forschungszwecke gedacht ist und nicht für den produktiven Einsatz verwendet werden soll

Datenstrukturen

Eine Datenstruktur ist eine bestimmte Art und Weise, Daten in einem Computer so zu organisieren und zu speichern, dass sie effizient erreicht und verändert werden können. Genauer gesagt, ist eine Datenstruktur eine Sammlung von Werten, den Beziehungen zwischen ihnen und den Funktionen oder Operationen, die auf die Daten angewendet werden können.

B - Anfänger:innen, A - Fortgeschrittene

B Verkettete Liste (Linked List)
B Doppelt verkettete Liste (Doubly Linked List)
B Warteschlange (Queue)
B Stapelspeicher (Stack)
B Hashtabelle (Hash Table)
B Heap-Algorithmus (Heap) - max und min Heap-Versionen
B Vorrangwarteschlange (Priority Queue)
A Trie (Trie)
A Baum (Tree)
A Binärer Suchbaum (Binary Search Tree)
A AVL-Baum (AVL Tree)
A Rot-Schwarz-Baum (Red-Black Tree)
A Segment-Baum (Segment Tree) - mit Min/Max/Summenbereich-Abfrage Beispiel
A Fenwick Baum (Fenwick Tree) (Binär indizierter Baum / Binary Indexed Tree)
A Graph (Graph) (sowohl gerichtet als auch ungerichtet)
A Union-Find-Struktur (Disjoint Set)
A Bloomfilter (Bloom Filter)

Algorithmen

Ein Algorithmus ist eine eindeutige Spezifikation, wie eine Klasse von Problemen zu lösen ist. Er besteht aus einem Satz von Regeln, die eine Abfolge von Operationen genau definieren.

B - Anfänger:innen, A - Fortgeschrittene

Algorithmen nach Thema

Mathe
B Bitmanipulation (Bit Manipulation) - Bits setzen/lesen/aktualisieren/löschen, Multiplikation/Division durch zwei negieren usw..
B Faktoriell (Factorial)
B Fibonacci-Zahl (Fibonacci Number) - Klassische und geschlossene Version
B Primfaktoren (Prime Factors) - Auffinden von Primfaktoren und deren Zählung mit Hilfe des Satz von Hardy-Ramanujan (Hardy-Ramanujan's theorem)
B Primzahl-Test (Primality Test) (Probedivision / trial division method)
B Euklidischer Algorithmus (Euclidean Algorithm) - Berechnen des größten gemeinsamen Teilers (ggT)
B Kleinstes gemeinsames Vielfaches (Least Common Multiple) (kgV)
B Sieb des Eratosthenes (Sieve of Eratosthenes) - Finden aller Primzahlen bis zu einer bestimmten Grenze
B Power of two (Is Power of Two) - Prüft, ob die Zahl eine Zweierpotenz ist (naive und bitweise Algorithmen)
B Pascalsches Dreieck (Pascal's Triangle)
B Komplexe Zahlen (Complex Number) - Komplexe Zahlen und Grundoperationen mit ihnen
B Bogenmaß & Grad (Radian & Degree) - Umrechnung von Bogenmaß in Grad und zurück
B Fast Powering Algorithmus (Fast Powering)
B Horner-Schema (Horner's method) - Polynomauswertung
B Matrizen (Matrices) - Matrizen und grundlegende Matrixoperationen (Multiplikation, Transposition usw.)
B Euklidischer Abstand (Euclidean Distance) - Abstand zwischen zwei Punkten/Vektoren/Matrizen
A Ganzzahlige Partitionierung (Integer Partition)
A Quadratwurzel (Square Root) - Newtonverfahren (Newton's method)
A Liu Hui π Algorithmus (Liu Hui π Algorithm) - Näherungsweise π-Berechnungen auf Basis von N-gons
A Diskrete Fourier-Transformation (Discrete Fourier Transform) - Eine Funktion der Zeit (ein Signal) in die Frequenzen zerlegen, aus denen sie sich zusammensetzt
Sets
B Kartesisches Produkt (Cartesian Product) - Produkt aus mehreren Mengen
B Fisher-Yates-Verfahren (Fisher–Yates Shuffle) - Zufällige Permutation einer endlichen Folge
A Potenzmenge (Power Set) - Alle Teilmengen einer Menge (Bitweise und Rücksetzverfahren Lösungen(backtracking solutions))
A Permutation (Permutations) (mit und ohne Wiederholungen)
A Kombination (Combinations) (mit und ohne Wiederholungen)
A Problem der längsten gemeinsamen Teilsequenz (Longest Common Subsequence) (LCS)
A Längste gemeinsame Teilsequenz (Longest Increasing Subsequence)
A Der kürzeste gemeinsame String (Shortest Common Supersequence) (SCS)
A Rucksackproblem (Knapsack Problem) - "0/1" und "Ungebunden"
A Das Maximum-Subarray Problem (Maximum Subarray) - "Brute-Force-Methode" und "Dynamische Programmierung" (Kadane' Algorithmus)
A Kombinationssumme (Combination Sum) - Alle Kombinationen finden, die eine bestimmte Summe bilden
Zeichenketten (Strings)
B Hamming-Abstand (Hamming Distance) - Anzahl der Positionen, an denen die Symbole unterschiedlich sind
A Levenshtein-Distanz (Levenshtein Distance) - Minimaler Editierabstand zwischen zwei Sequenzen
A Knuth-Morris-Pratt-Algorithmus (Knuth–Morris–Pratt Algorithm) (KMP Algorithmus) - Teilstringsuche (Mustervergleich / Pattern Matching)
A Z-Algorithmus (Z Algorithm) - Teilstringsuche (Mustervergleich / Pattern Matching)
A Rabin-Karp-Algorithmus (Rabin Karp Algorithm) - Teilstringsuche
A Längstes häufiges Teilzeichenfolgenproblem (Longest Common Substring)
A Regulärer Ausdruck (Regular Expression Matching)
Suchen
B Lineare Suche (Linear Search)
B Sprungsuche (Jump Search) (oder Blocksuche) - Suche im sortierten Array
B Binäre Suche (Binary Search) - Suche in einem sortierten Array
B Interpolationssuche (Interpolation Search) - Suche in gleichmäßig verteilt sortiertem Array
Sortieren
B Bubblesort (Bubble Sort)
B Selectionsort (Selection Sort)
B Einfügesortierenmethode (Insertion Sort)
B Haldensortierung (Heap Sort)
B Mergesort (Merge Sort)
B Quicksort (Quicksort) - in-place und non-in-place Implementierungen
B Shellsort (Shellsort)
B Countingsort (Counting Sort)
B Fachverteilen (Radix Sort)
Verkettete Liste (Linked List)
B Gerade Traversierung (Straight Traversal)
B Umgekehrte Traversierung (Reverse Traversal)
Bäume
B Tiefensuche (Depth-First Search) (DFS)
B Breitensuche (Breadth-First Search) (BFS)
Graphen
B Tiefensuche (Depth-First Search) (DFS)
B Breitensuche (Breadth-First Search) (BFS)
B Algorithmus von Kruskal (Kruskal’s Algorithm) - Finden des Spannbaum (Minimum Spanning Tree / MST) für einen gewichteten ungerichteten Graphen
A Dijkstra-Algorithmus (Dijkstra Algorithm) - Finden der kürzesten Wege zu allen Knoten des Graphen von einem einzelnen Knotenpunkt aus
A Bellman-Ford-Algorithmus (Bellman-Ford Algorithm) - Finden der kürzesten Wege zu allen Knoten des Graphen von einem einzelnen Knotenpunkt aus
A Algorithmus von Floyd und Warshall (Floyd-Warshall Algorithm) - Die kürzesten Wege zwischen allen Knotenpaaren finden
A Zykluserkennung (Detect Cycle) - Sowohl für gerichtete als auch für ungerichtete Graphen (DFS- und Disjoint-Set-basierte Versionen)
A Algorithmus von Prim (Prim’s Algorithm) - Finden des Spannbaums (Minimum Spanning Tree / MST) für einen gewichteten ungerichteten Graphen
A Topologische Sortierung (Topological Sorting) - DFS-Verfahren
A Artikulationspunkte (Articulation Points) - Algorithmus von Tarjan (Tarjan's algorithm) (DFS basiert)
A Brücke (Bridges) - DFS-basierter Algorithmus
A Eulerkreisproblem (Eulerian Path and Eulerian Circuit) - Algorithmus von Fleury (Fleury's algorithm) - Jede Kante genau einmal durchlaufen.
A Hamiltonkreisproblem (Hamiltonian Cycle) - Jeden Eckpunkt genau einmal durchlaufen.
A Starke Zusammenhangskomponente (Strongly Connected Components) - Kosarajus Algorithmus
A Problem des Handlungsreisenden (Travelling Salesman Problem) - Kürzestmögliche Route, die jede Stadt besucht und zur Ausgangsstadt zurückkehrt
Kryptographie
B Polynomiale Streuwertfunktion(Polynomial Hash) - Rollierende Streuwert-Funktion basierend auf Polynom
B Schienenzaun Chiffre (Rail Fence Cipher) - Ein Transpositionsalgorithmus zur Verschlüsselung von Nachrichten
B Caesar-Verschlüsselung (Caesar Cipher) - Einfache Substitutions-Chiffre
B Hill-Chiffre (Hill Cipher) - Substitutionschiffre basierend auf linearer Algebra
Maschinelles Lernen
B Künstliches Neuron (NanoNeuron) - 7 einfache JS-Funktionen, die veranschaulichen, wie Maschinen tatsächlich lernen können (Vorwärts-/Rückwärtspropagation)
B Nächste-Nachbarn-Klassifikation (k-NN) - k-nächste-Nachbarn-Algorithmus
B k-Means (k-Means) - k-Means-Algorithmus
Image Processing
B Inhaltsabhängige Bildverzerrung (Seam Carving) - Algorithmus zur inhaltsabhängigen Bildgrößenänderung
Unkategorisiert
B Türme von Hanoi (Tower of Hanoi)
B Rotationsmatrix (Square Matrix Rotation) - In-Place-Algorithmus
B Jump Game (Jump Game) - Backtracking, dynamische Programmierung (Top-down + Bottom-up) und gierige Beispiele
B Eindeutige Pfade (Unique Paths) - Backtracking, dynamische Programmierung und Pascalsches Dreieck basierte Beispiele
B Regenterrassen (Rain Terraces) - Auffangproblem für Regenwasser (trapping rain water problem) (dynamische Programmierung und Brute-Force-Versionen)
B Rekursive Treppe (Recursive Staircase) - Zählen der Anzahl der Wege, die nach oben führen (4 Lösungen)
B Beste Zeit zum Kaufen/Verkaufen von Aktien (Best Time To Buy Sell Stocks) - Beispiele für "Teile und Herrsche" und Beispiele für den One-Pass-Algorithmus
A Damenproblem (N-Queens Problem)
A Springerproblem (Knight's Tour)

Algorithmen nach Paradigma

Ein algorithmisches Paradigma ist eine generische Methode oder ein Ansatz, der dem Entwurf einer Klasse von Algorithmen zugrunde liegt. Es ist eine Abstraktion, die höher ist als der Begriff des Algorithmus. Genauso wie ein Algorithmus eine Abstraktion ist, die höher ist als ein Computerprogramm.

Brachiale Gewalt (Brute Force) - schaut sich alle Möglichkeiten an und wählt die beste Lösung aus
B Lineare Suche (Linear Search)
B Regenterrassen (Rain Terraces) - Auffangproblem für Regenwasser (trapping rain water problem) (dynamische Programmierung und Brute-Force-Versionen)
B Rekursive Treppe (Recursive Staircase) - Zählen der Anzahl der Wege, die nach oben führen (4 Lösungen)
A Das Maximum-Subarray Problem (Maximum Subarray)
A Problem des Handlungsreisenden (Travelling Salesman Problem) - Kürzestmögliche Route, die jede Stadt besucht und zur Ausgangsstadt zurückkehrt
A Diskrete Fourier-Transformation (Discrete Fourier Transform) - Eine Funktion der Zeit (ein Signal) in die Frequenzen zerlegen, aus denen sie sich zusammensetzt
Gierig (Greedy) - Wählt die beste Option zum aktuellen Zeitpunkt, ohne Rücksicht auf die Zukunft
B Jump Game (Jump Game)
A Rucksackproblem (Unbound Knapsack Problem)
A Dijkstra-Algorithmus (Dijkstra Algorithm) - Finden der kürzesten Wege zu allen Knoten des Graphen von einem einzelnen Knotenpunkt aus
A Algorithmus von Prim (Prim’s Algorithm) - Finden des Spannbaums (Minimum Spanning Tree / MST) für einen gewichteten ungerichteten Graphen
B Algorithmus von Kruskal (Kruskal’s Algorithm) - Finden des Spannbaum (Minimum Spanning Tree / MST) für einen gewichteten ungerichteten Graphen
Teile und herrsche - Das Problem in kleinere Teile aufteilen und diese Teile dann lösen
B Binäre Suche (Binary Search)
B Türme von Hanoi (Tower of Hanoi)
B Pascalsches Dreieck (Pascal's Triangle)
B Euklidischer Algorithmus (Euclidean Algorithm) - calculate the Greatest Common Divisor (GCD)
B Mergesort (Merge Sort)
B Quicksort (Quicksort)
B Tiefensuche (Depth-First Search) (DFS)
B Breitensuche (Breadth-First Search) (DFS)
B Matrizen (Matrices) - Matrizen und grundlegende Matrixoperationen (Multiplikation, Transposition usw.)
B Jump Game (Jump Game)
B Fast Powering Algorithmus (Fast Powering)
B Beste Zeit zum Kaufen/Verkaufen von Aktien (Best Time To Buy Sell Stocks) - Beispiele für "Teile und Herrsche" und Beispiele für den One-Pass-Algorithmus
A Permutation (Permutations) (mit und ohne Wiederholungen)
A Kombination (Combinations) (mit und ohne Wiederholungen)
Dynamische Programmierung - Eine Lösung aus zuvor gefundenen Teillösungen aufbauen
B Fibonacci-Zahl (Fibonacci Number)
B Jump Game (Jump Game)
B Eindeutige Pfade (Unique Paths)
B Regenterrassen (Rain Terraces) - Auffangproblem für Regenwasser (trapping rain water problem) (dynamische Programmierung und Brute-Force-Versionen)
B Rekursive Treppe (Recursive Staircase) - Zählen der Anzahl der Wege, die nach oben führen (4 Lösungen)
B Inhaltsabhängige Bildverzerrung (Seam Carving) - Algorithmus zur inhaltsabhängigen Bildgrößenänderung
A Levenshtein-Distanz (Levenshtein Distance) - Minimaler Editierabstand zwischen zwei Sequenzen
A Problem der längsten gemeinsamen Teilsequenz (Longest Common Subsequence) (LCS)
A Längstes häufiges Teilzeichenfolgenproblem (Longest Common Substring)
A Längste gemeinsame Teilsequenz (Longest Increasing Subsequence)
A Der kürzeste gemeinsame String (Shortest Common Supersequence)
A Rucksackproblem (0/1 Knapsack Problem)
A Ganzzahlige Partitionierung (Integer Partition)
A Das Maximum-Subarray Problem (Maximum Subarray)
A Bellman-Ford-Algorithmus (Bellman-Ford Algorithm) - Finden der kürzesten Wege zu allen Knoten des Graphen von einem einzelnen Knotenpunkt aus
A Algorithmus von Floyd und Warshall (Floyd-Warshall Algorithm) - Die kürzesten Wege zwischen allen Knotenpaaren finden
A Regulärer Ausdruck (Regular Expression Matching)
Zurückverfolgung - Ähnlich wie bei Brute-Force versuchen Sie, alle möglichen Lösungen zu generieren, aber jedes Mal, wenn Sie die nächste Lösung generieren, testen Sie, ob sie alle Bedingungen erfüllt, und fahren erst dann mit der Generierung weiterer Lösungen fort. Andernfalls gehen Sie zurück und nehmen einen anderen Weg, um eine Lösung zu finden. Normalerweise wird das DFS-Traversal des Zustandsraums verwendet.
B Jump Game (Jump Game)
B Eindeutige Pfade (Unique Paths)
A Potenzmenge (Power Set) - Alle Teilmengen einer Menge
A Hamiltonkreisproblem (Hamiltonian Cycle) - Jeden Eckpunkt genau einmal durchlaufen.
A Damenproblem (N-Queens Problem)
A Springerproblem (Knight's Tour)
A Kombinationssumme (Combination Sum) - Alle Kombinationen finden, die eine bestimmte Summe bilden
Verzweigung & Bindung - Merkt sich die Lösung mit den niedrigsten Kosten, die in jeder Phase der Backtracking-Suche gefunden wurde, und verwendet die Kosten der bisher gefundenen Lösung mit den niedrigsten Kosten als untere Schranke für die Kosten einer Lösung des Problems mit den geringsten Kosten, um Teillösungen zu verwerfen, deren Kosten größer sind als die der bisher gefundenen Lösung mit den niedrigsten Kosten. Normalerweise wird das BFS-Traversal in Kombination mit dem DFS-Traversal des Zustandsraumbaums verwendet.

So verwendest du dieses Repository

Alle Abhängigkeiten installieren

npm install

ESLint ausführen

You may want to run it to check code quality.

npm run lint

Alle Tests ausführen

npm test

Tests nach Namen ausführen

npm test -- 'LinkedList'

Fehlerbehebung

Falls das Linting oder Testen fehlschlägt, versuche, den Ordner "node_modules" zu löschen und die npm-Pakete neu zu installieren:

rm -rf ./node_modules
npm i

Spielwiese

Du kannst mit Datenstrukturen und Algorithmen in der Datei ./src/playground/playground.js herumspielen und dir in dieser Datei Tests schreiben ./src/playground/__test__/playground.test.js.

Dann führe einfach folgenden Befehl aus, um zu testen, ob dein Spielwiesencode wie erwartet funktioniert:

npm test -- 'playground'

Nützliche Informationen

Referenzen

▶ Datenstrukturen und Algorithmen auf YouTube(Englisch)

O-Notation (Big O Notation)

Die O-Notation wird verwendet, um Algorithmen danach zu klassifizieren, wie ihre Laufzeit oder ihr Platzbedarf mit zunehmender Eingabegröße wächst. In der folgenden Tabelle finden Sie die häufigsten Wachstumsordnungen von Algorithmen, die in Big-O-Notation angegeben sind.

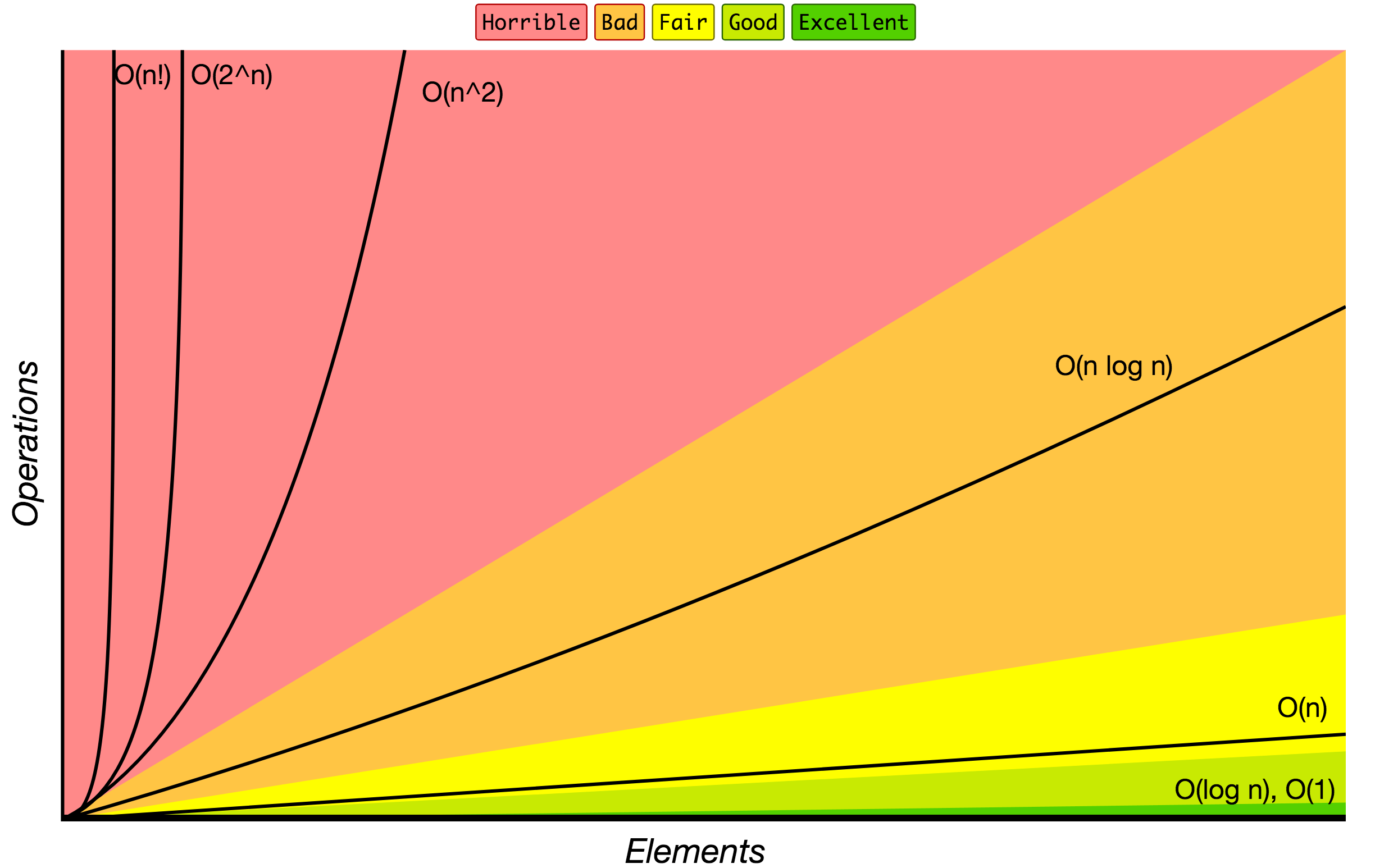
O-Notation Graphen

Quelle: Big O Cheat Sheet.

Nachfolgend finden Sie eine Liste einiger der am häufigsten verwendeten Big O-Notationen und deren Leistungsvergleiche für unterschiedliche Größen der Eingabedaten.

Big O Notation	Berechnungen für 10 Elemente	Berechnungen für 100 Elemente	Berechnungen für 1000 Elemente
O(1)	1	1	1
O(log N)	3	6	9
O(N)	10	100	1000
O(N log N)	30	600	9000
O(N^2)	100	10000	1000000
O(2^N)	1024	1.26e+29	1.07e+301
O(N!)	3628800	9.3e+157	4.02e+2567

Komplexität von Datenstrukturoperationen

Datenstruktur	Zugriff auf	Suche	Einfügen	Löschung	Kommentare
Array	1	n	n	n
Stack	n	n	1	1
Queue	n	n	1	1
Linked List	n	n	1	n
Hash Table	-	n	n	n	Im Falle einer perfekten Hash-Funktion wären die Kosten O(1)
Binary Search Tree	n	n	n	n	Im Falle eines ausgeglichenen Baumes wären die Kosten O(log(n))
B-Tree	log(n)	log(n)	log(n)	log(n)
Red-Black Tree	log(n)	log(n)	log(n)	log(n)
AVL Tree	log(n)	log(n)	log(n)	log(n)
Bloom Filter	-	1	1	-	Falschpostive sind bei der Suche möglichen

Komplexität von Array-Sortieralgorithmen

Name	Bester	Durchschnitt	Schlechtester	Speicher	Stabil	Kommentar
Bubble sort	n	n²	n²	1	JA
Insertion sort	n	n²	n²	1	Ja
Selection sort	n²	n²	n²	1	Nein
Heap sort	n log(n)	n log(n)	n log(n)	1	Nein
Merge sort	n log(n)	n log(n)	n log(n)	n	Ja
Quick sort	n log(n)	n log(n)	n²	log(n)	Nein	Quicksort wird normalerweise in-place mit O(log(n)) Stapelplatz ausgeführt
Shell sort	n log(n)	abhängig von Spaltfolge	n (log(n))²	1	Nein
Counting sort	n + r	n + r	n + r	n + r	Ja	r - größte Zahl im Array
Radix sort	n * k	n * k	n * k	n + k	Ja	k - Länge des längsten Schlüssels

Projekt-Unterstützer

Du kannst dieses Projekt unterstützen über ❤️️ GitHub or ❤️️ Patreon.

Leute, die dieses Projekt unterstützen ∑ = 0

ℹ️ A few more projects and articles about JavaScript and algorithms on trekhleb.dev