JavaScriptアルゴリズムとデータ構造

このリポジトリには、JavaScriptベースの一般的なアルゴリズムとデータ構造に関する多数のサンプルが含まれています。

各アルゴリズムとデータ構造には独自のREADMEがあります。関連する説明、そして参考資料 (YouTube動画)も含まれています。

Read this in other languages: English, 简体中文, 繁體中文, 한국어, Polski, Français, Español, Português, Русский, Türk, Italiana, Bahasa Indonesia, Українська, Arabic, Tiếng Việt, Deutsch, Uzbek

データ構造

データ構造は、データ値、データ値との間の関係、そして、データを扱うことができる関数と演算の集合で、データを特定の方法で構成して保存することで、より効率的にアクセスして変更することができます。

B - 初心者, A - 上級

B リンクされたリスト
B 二重リンクリスト
B キュー
B スタック
B ハッシュ表
B ヒープ - max and min heap versions
B 優先度キュー
A トライ
A ツリー
A バイナリ検索ツリー
A AVLツリー
A 赤黒のツリー
A セグメントツリー - with min/max/sum range queries examples
A フェンウィック・ツリー (Binary Indexed Tree)
A グラフ (both directed and undirected)
A 分離集合
A ブルームフィルタ

アルゴリズム

アルゴリズムとは、問題のクラスをどのように解決するかの明確な仕様です。一連の操作を正確に定義する一連のルールです。

B - 初心者, A - 上級

トピック別アルゴリズム

数学
B ビット操作 - set/get/update/clear bits, 2つの乗算/除算, 否定的にする. 等
B 因果関係
B フィボナッチ数 - クラシックとクローズドフォームのバージョン
B 素数性テスト (trial division 方法)
B ユークリッドアルゴリズム - 最大公約数を計算する (GCD)
B 最小公倍数 (LCM)
B エラトステネスのふるい - 与えられた限度まですべての素数を見つける
B Is Power of Two - 数値が2の累乗であるかどうかを調べる（単純なアルゴリズムとビットごとのアルゴリズム）
B パスカルの三角形
B 複素数 - 複素数とその基本演算
B ラジアン＆度 - 度数と逆方向の変換に対するラジアン
B 高速電力供給
A 整数パーティション
A Liu Hui π アルゴリズム - N-gonsに基づく近似π計算
A 離散フーリエ変換 - 時間（信号）の関数をそれを構成する周波数に分解する
セット
B デカルト積 - 複数の積の積
B Fisher–Yates Shuffle - 有限シーケンスのランダム置換
A パワーセット - セットのすべてのサブセット（ビットごとのソリューションとバックトラッキングソリューション）
A 順列（繰り返しの有無にかかわらず）
A 組み合わせ（繰返しあり、繰返しなし）
A 最長共通部分列 (LCS)
A 最長増加サブシーケンス
A 最短共通スーパーシーケンス (SCS)
A ナップザック問題 - 「0/1」と「非結合」問題
A 最大サブアレイ - 「ブルートフォース」と「ダイナミックプログラミング」（Kadane's版）
A 組み合わせ合計 - 特定の合計を構成するすべての組み合わせを見つける
文字列
B ハミング距離 - シンボルが異なる位置の数
A レーベンシュタイン距離 - 2つのシーケンス間の最小編集距離
A Knuth-Morris-Prattアルゴリズム (KMP Algorithm) - 部分文字列検索 (pattern matching)
A Z アルゴリズム - 部分文字列検索 (pattern matching)
A Rabin Karpアルゴリズム - 部分文字列検索
A 最長共通部分文字列
A 正規表現マッチング
検索
B リニアサーチ
B ジャンプ検索 (Jump Search) - ソートされた配列で検索
B バイナリ検索 - ソートされた配列で検索
B 補間探索 - 一様分布のソート配列で検索する
並べ替え
B バブルソート
B 選択ソート
B 挿入ソート
B ヒープソート
B マージソート
B クイックソート -インプレースおよび非インプレース・インプリメンテーション
B シェルソート
B 並べ替えを数える
B 基数ソート
リンクされたリスト
B ストレートトラバーサル
B 逆方向のトラバーサル
ツリー
B 深度優先検索 (DFS)
B 幅優先検索 (BFS)
グラフ
B 深度優先検索 (DFS)
B 幅優先検索 (BFS)
B Kruskalのアルゴリズム - 重み付き無向グラフの最小スパニングツリー（MST）の発見
A Dijkstraアルゴリズム - 単一の頂点からすべてのグラフ頂点への最短経路を見つける
A Bellman-Fordアルゴリズム - 単一の頂点からすべてのグラフ頂点への最短経路を見つける
A Floyd-Warshallアルゴリズム - すべての頂点ペア間の最短経路を見つける
A Detect Cycle - 有向グラフと無向グラフの両方（DFSおよびディスジョイントセットベースのバージョン）
A プリムのアルゴリズム - 重み付き無向グラフの最小スパニングツリー（MST）の発見
A トポロジカルソート - DFSメソッド
A アーティキュレーションポイント - Tarjanのアルゴリズム（DFSベース）
A ブリッジ - DFSベースのアルゴリズム
A オイラーパスとオイラー回路 - フルリーアルゴリズム - すべてのエッジを正確に1回訪問する
A ハミルトニアンサイクル - すべての頂点を正確に1回訪問する
A 強連結成分 - コサラジュのアルゴリズム
A トラベリングセールスマン問題 - 各都市を訪問し、起点都市に戻る最短経路
暗号
B 多項式ハッシュ - 関数多項式に基づくハッシュ関数
未分類
B ハノイの塔
B 正方行列回転 - インプレイスアルゴリズム
B ジャンプゲーム - バックトラック、ダイナミックプログラミング（トップダウン+ボトムアップ）、欲張りの例
B ユニークなパス - バックトラック、動的プログラミング、PascalのTriangleベースの例
B レインテラス - トラップ雨水問題（ダイナミックプログラミングとブルートフォースバージョン）
B 再帰的階段 - 上に到達する方法の数を数える（4つのソリューション）
A N-クイーンズ問題
A ナイトツアー

Paradigmによるアルゴリズム

アルゴリズムパラダイムは、あるクラスのアルゴリズムの設計の基礎をなす一般的な方法またはアプローチである。それは、アルゴリズムがコンピュータプログラムよりも高い抽象であるのと同様に、アルゴリズムの概念よりも高い抽象である。 * ブルートフォース - すべての可能性を見て最適なソリューションを選択する * B 線形探索 * B レインテラス - 雨水問題 * B Recursive Staircase - 先頭に到達する方法の数を数えます * A 最大サブアレイ * A 旅行セールスマン問題 - 各都市を訪れ、起点都市に戻る最短ルート * A 離散フーリエ変換 - 時間（信号）の関数をそれを構成する周波数に分解する * 欲張り - 未来を考慮することなく、現時点で最適なオプションを選択する * B ジャンプゲーム * A 結合されていないナップザック問題 * A Dijkstra Algorithm - すべてのグラフ頂点への最短経路を見つける * A Prim’s Algorithm - 重み付き無向グラフの最小スパニングツリー（MST）を見つける * A Kruskalのアルゴリズム - 重み付き無向グラフの最小スパニングツリー（MST）を見つける * 分割と征服 - 問題をより小さな部分に分割し、それらの部分を解決する * B バイナリ検索 * B ハノイの塔 * B パスカルの三角形 * B ユークリッドアルゴリズム - GCD（Greatest Common Divisor）を計算する * B マージソート * B クイックソート * B ツリーの深さ優先検索 (DFS) * B グラフの深さ優先検索 (DFS) * B ジャンプゲーム * B 高速電力供給 * A 順列（繰り返しの有無にかかわらず） * A 組み合わせ（繰返しあり、繰返しなし） * 動的プログラミング - 以前に発見されたサブソリューションを使用してソリューションを構築する * B フィボナッチ数 * B ジャンプゲーム * B ユニークなパス * B 雨テラス - トラップ雨水問題 * B 再帰的階段 - 上に到達する方法の数を数える * A Levenshtein Distance - 2つのシーケンス間の最小編集距離 * A 最長共通部分列 (LCS) * A 最長共通部分文字列 * A 最長増加サブシーケンス * A 最短共通共通配列 * A 0/1ナップザック問題 * A 整数パーティション * A 最大サブアレイ * A Bellman-Fordアルゴリズム - すべてのグラフ頂点への最短経路を見つける * A Floyd-Warshallアルゴリズム - すべての頂点ペア間の最短経路を見つける * A 正規表現マッチング * バックトラッキング - ブルートフォースと同様に、可能なすべてのソリューションを生成しようとしますが、次のソリューションを生成するたびにすべての条件を満たすかどうかをテストし、それ以降は引き続きソリューションを生成します。それ以外の場合は、バックトラックして、解決策を見つける別の経路に進みます。通常、状態空間のDFSトラバーサルが使用されています。 * B ジャンプゲーム * B ユニークなパス * B パワーセット - セットのすべてのサブセット * A ハミルトニアンサイクル - すべての頂点を正確に1回訪問する * A N-クイーンズ問題 * A ナイトツアー * A 組み合わせ合計 - 特定の合計を構成するすべての組み合わせを見つける * ブランチ＆バウンド - バックトラック検索の各段階で見つかった最もコストの低いソリューションを覚えておいて、最もコストの低いソリューションのコストを使用します。これまでに発見された最もコストの低いソリューションよりも大きなコストで部分ソリューションを破棄するように指示します。通常、状態空間ツリーのDFSトラバーサルと組み合わせたBFSトラバーサルが使用されています。

このリポジトリの使い方

すべての依存関係をインストールする

npm install

ESLintを実行する

これを実行してコードの品質をチェックすることができます。

npm run lint

すべてのテストを実行する

npm test

名前でテストを実行する

npm test -- 'LinkedList'

playground

データ構造とアルゴリズムを ./src/playground/playground.js ファイルで再生し、それに対するテストを書くことができ ./src/playground/__test__/playground.test.js.

次に、次のコマンドを実行して、遊び場コードが正常に動作するかどうかをテストします。

npm test -- 'playground'

有用な情報

参考文献

▶ データ構造とアルゴリズム on YouTube

ビッグO表記

Big O表記法は 入力サイズが大きくなるにつれて実行時間やスペース要件がどのように増加するかに応じてアルゴリズムを分類するために使用されます。下のチャートでは、Big O表記で指定されたアルゴリズムの成長の最も一般的な順序を見つけることができます。

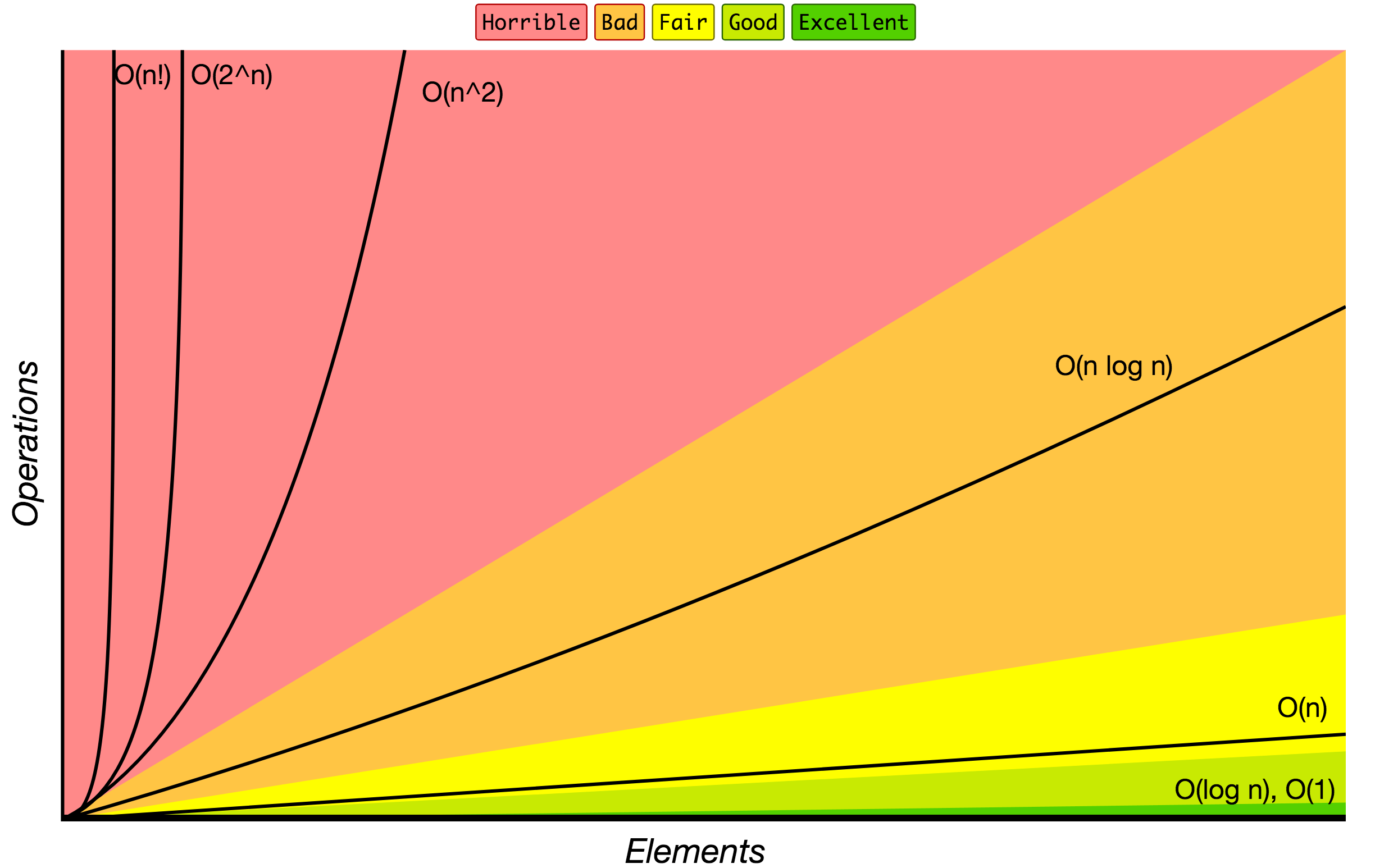
Big Oグラフ

出典: Big Oチートシート.

以下は、最も使用されているBig O表記のリストと、入力データのさまざまなサイズに対するパフォーマンス比較です。

Big O Notation	Computations for 10 elements	Computations for 100 elements	Computations for 1000 elements
O(1)	1	1	1
O(log N)	3	6	9
O(N)	10	100	1000
O(N log N)	30	600	9000
O(N^2)	100	10000	1000000
O(2^N)	1024	1.26e+29	1.07e+301
O(N!)	3628800	9.3e+157	4.02e+2567

データ構造操作の複雑さ

Data Structure	Access	Search	Insertion	Deletion	Comments
Array	1	n	n	n
Stack	n	n	1	1
Queue	n	n	1	1
Linked List	n	n	1	1
Hash Table	-	n	n	n	In case of perfect hash function costs would be O(1)
Binary Search Tree	n	n	n	n	In case of balanced tree costs would be O(log(n))
B-Tree	log(n)	log(n)	log(n)	log(n)
Red-Black Tree	log(n)	log(n)	log(n)	log(n)
AVL Tree	log(n)	log(n)	log(n)	log(n)
Bloom Filter	-	1	1	-	False positives are possible while searching

配列の並べ替えアルゴリズムの複雑さ

Name	Best	Average	Worst	Memory	Stable	Comments
Bubble sort	n	n²	n²	1	Yes
Insertion sort	n	n²	n²	1	Yes
Selection sort	n²	n²	n²	1	No
Heap sort	n log(n)	n log(n)	n log(n)	1	No
Merge sort	n log(n)	n log(n)	n log(n)	n	Yes
Quick sort	n log(n)	n log(n)	n²	log(n)	No	Quicksort is usually done in-place with O(log(n)) stack space
Shell sort	n log(n)	depends on gap sequence	n (log(n))²	1	No
Counting sort	n + r	n + r	n + r	n + r	Yes	r - biggest number in array
Radix sort	n * k	n * k	n * k	n + k	Yes	k - length of longest key

ℹ️ A few more projects and articles about JavaScript and algorithms on trekhleb.dev