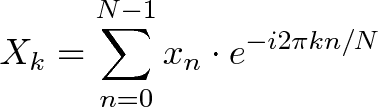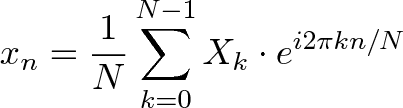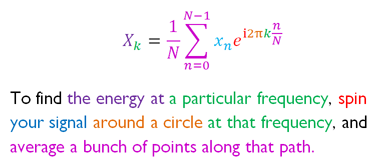首页
▼ 算法合集
▼ 加密算法
▼ 凯撒密码
凯撒密码
▼ Hill密码算法
Hill密码算法
▼ 多项式哈希算法
多项式哈希算法
▼ Rail Fence Cipher
Rail Fence Cipher
▼ Graph算法
▼ 关节点
关节点
▼ Bellman-Ford算法
Bellman-Ford算法
▼ 广度优先搜索
广度优先搜索
▼ GraphBridges
桥接模式
▼ 深度优先搜索
深度优先搜索
▼ 检测循环
检测循环
▼ Dijkstra算法
Dijkstra算法
▼ Eulerian Path
欧拉路径
▼ Floyd-Warshall算法
Floyd-Warshall算法
▼ HamiltonianCycle
Hamiltonian Cycle
▼ Kruskal算法
Kruskal算法
▼ Prim算法
Prim算法
▼ 强连通分量
强连通分量
▼ 拓扑排序
拓扑排序
▼ Travelling Salesman Problem
Travelling Salesman
▼ 图像处理算法
▼ Seam Carving算法
内容感知缩放算法
▼ 链表
▼ 反向遍历
反向遍历
▼ GraphTraversal
GraphTraversal
▼ 数学算法
▼ 二进制浮点数
BinaryFloatingPoint
▼ 位操作
位操作算法
▼ 复数
复数
▼ 欧几里得算法
Euclidean Algorithm
▼ Euclidean Distance
欧几里得距离
▼ 阶乘算法
阶乘算法
▼ 快速幂算法
快速幂算法
▼ Fibonacci数列
斐波那契数列
▼ 傅里叶变换
Fourier变换
▼ Horner法
霍纳法则
▼ 整数划分
整数划分
▼ 判断是否为2的幂
判断是否为2的幂
▼ 最小公倍数
最小公倍数
▼ Liu Hui
Liu Hui
▼ 矩阵
Matrix
▼ Pascal三角形
Pascal三角形
▼ Primality Test
素数测试
▼ 质因数
质因数
▼ 弧度计算
弧度计算
▼ 埃拉托色尼筛法
埃拉托色尼筛法
▼ SquareRoot
SquareRoot
▼ MachineLearning
▼ K均值算法
K均值算法
▼ K近邻算法
K近邻算法
▼ 搜索算法
▼ 二分查找算法
二分查找
▼ 插值搜索算法
插值搜索算法
▼ 跳跃搜索算法
跳跃搜索算法
▼ 线性搜索
线性搜索算法
▼ 集合
▼ 笛卡尔积
笛卡尔积
▼ 组合总和
组合总和
▼ 组合算法
组合算法
▼ Fisher-Yates洗牌算法
Fisher-Yates洗牌算法
▼ 背包问题
背包问题
▼ 最长公共子序列
最长公共子序列
▼ 最长递增子序列
最长递增子序列
▼ 最大子数组
最大子数组
▼ 排列组合
排列组合
▼ 幂集
幂集算法
▼ 最短公共超序列
最短公共超序列
▼ Sorting Algorithms
▼ 冒泡排序
冒泡排序
▼ 桶排序算法
桶排序算法
▼ 计数排序算法
计数排序
▼ 堆排序算法
堆排序
▼ 插入排序
插入排序
▼ 归并排序
归并排序
▼ 快速排序算法
快速排序算法
▼ 基数排序
基数排序
▼ 选择排序算法
选择排序算法
▼ 希尔排序
希尔排序
▼ 统计学
▼ 加权随机
加权随机算法
▼ 字符串算法
▼ Hamming距离
Hamming距离
▼ KnuthMorrisPratt算法
Knuth-Morris-Pratt算法
▼ LevenshteinDistance
Levenshtein距离
▼ 最长公共子串
最长公共子串
▼ 回文检测算法
回文检测算法
▼ Rabin-Karp算法
Rabin-Karp算法
▼ 正则表达式匹配
正则表达式匹配
▼ Z算法
Z算法
▼ Tree Data Structure
▼ 广度优先搜索
广度优先搜索
▼ 深度优先搜索
深度优先搜索
▼ 未分类
▼ 最佳买卖股票时机
最佳买卖股票时机
▼ 汉诺塔算法
HanoiTower
▼ 跳跃游戏算法
跳跃游戏
▼ KnightTour
骑士巡逻
▼ N皇后问题
N皇后问题
▼ 雨水收集
雨水收集
▼ 递归楼梯问题
递归楼梯问题
▼ 方阵旋转
方阵旋转
▼ 独特路径
UniquePaths
▼ 数据结构
▼ BloomFilter算法
布隆过滤器
▼ 不相交集数据结构
Disjoint Set
▼ 双向链表
双向链表
▼ Graph
Graph算法
▼ 哈希表
哈希表
▼ Heap数据结构
Heap数据结构
▼ 链表
链表
▼ LRU缓存
LRU缓存
▼ 优先队列
优先队列
▼ 队列
队列
▼ 栈结构
栈结构
▼ Tree Data Structure
树结构
▼ AVL树
AVL树
▼ 二叉搜索树
二叉搜索树
▼ Fenwick树
Fenwick树
▼ 红黑树
红黑树
▼ 线段树
SegmentTree
▼ Trie数据结构
Trie数据结构
傅里叶变换
在其他语言中阅读:
法语。
定义
傅里叶变换(FT)将时间函数(信号)分解为其组成部分的频率,类似于如何用构成和弦的音符的频率(或音高)来表达音乐和弦。
离散傅里叶变换(DFT)将函数的有限等间隔样本序列转换为相同长度的离散时间傅里叶变换(DTFT)序列,后者是频率的复值函数。DTFT采样的间隔是输入序列持续时间的倒数。逆DFT是一个傅里叶级数,使用DTFT样本作为在相应DTFT频率处的复正弦波的系数。它具有与原始输入序列相同的样本值。因此,DFT被认为是原始输入序列的频域表示。如果原始序列跨越了函数的所有非零值,其DTFT是连续的(和周期性的),并且DFT提供了周期的一个循环的离散样本。如果原始序列是周期性函数的一个周期,DFT提供了DTFT周期的所有非零值。
离散傅里叶变换将N个复数序列转换为一个复数序列:
{xn} = x0, x1, x2 ..., xN-1
转换为另一个复数序列:
{Xk} = X0, X1, X2 ..., XN-1
由以下公式定义:

离散时间傅里叶变换(DTFT)是一种傅里叶分析形式,适用于连续函数的均匀间隔样本。术语离散时间指的是变换操作于通常具有时间单位的离散数据(样本)。仅从这些样本中,它产生了一个频率的函数,这是原始连续函数的连续傅里叶变换的周期性求和。
快速傅里叶变换(FFT)是一种算法,它在时间(或空间)周期内对信号进行采样,并将其分解为它的频率分量。这些分量是在不同频率的单个正弦振荡,每个都有自己独特的振幅和相位。
这个变换在下面的图中进行了说明。在图中测量的时间段内,信号包含3个不同的主导频率。
时间和频率域中的信号视图:
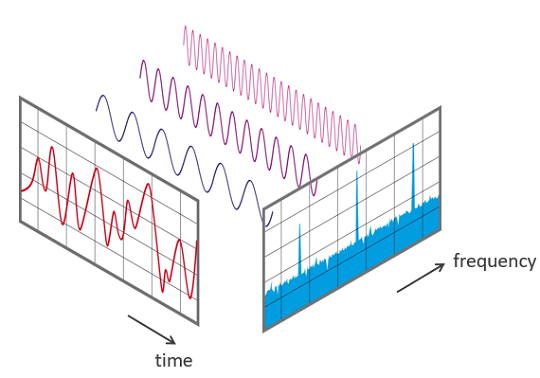
FFT算法计算序列的离散傅里叶变换(DFT)或其逆变换(IFFT)。傅里叶分析将信号从其原始域转换到频域的表示,反之亦然。FFT通过将DFT矩阵分解为稀疏(主要是零)因子的乘积,迅速计算此类变换。因此,它成功地降低了计算DFT的复杂性,从如果直接应用DFT的定义产生的O(n2),到O(n log n),其中n是数据大小。
这里是对10、20、30、40和50 Hz余弦波之和的离散傅里叶分析:
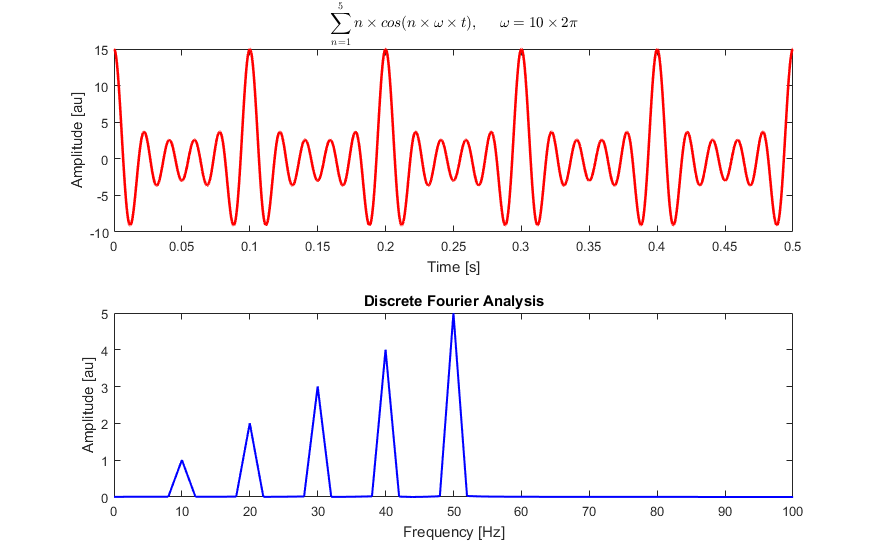
解释
傅里叶变换是迄今为止最深刻的洞察之一。不幸的是,含义被埋藏在复杂的方程中:
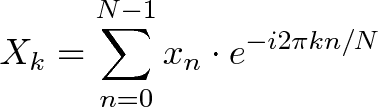
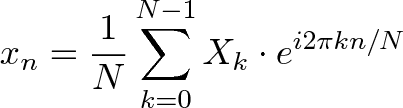
与其跳入符号,不如亲自体验关键思想。这里有一个简单的比喻:
- 傅里叶变换能做什么? 给定一杯奶昔,它找到食谱。
- 怎么做? 将奶昔通过过滤器提取每个成分。
- 为什么? 食谱比奶昔本身更容易分析、比较和修改。
- 我们怎么找回奶昔? 混合成分。
用圆圈思考,而不仅仅是正弦波
傅里叶变换关注的是圆形路径(而不是1维正弦波),欧拉公式是一种巧妙的方式来生成它们:
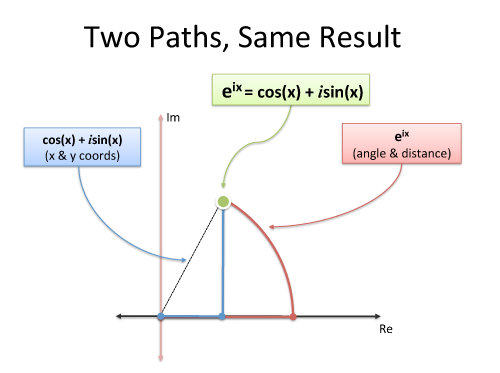
我们必须使用虚指数来绕圈走吗?不,但这很方便且紧凑。当然,我们可以描述我们的路径为在两个维度(实部和虚部)中的协调运动,但不要忘记大局:我们只是在绕圈走。
发现完整的变换
重要的见解:我们的信号只是一系列时间尖峰!如果我们合并每个时间尖峰的食谱,我们应该得到完整信号的食谱。
傅里叶变换逐频率构建食谱:
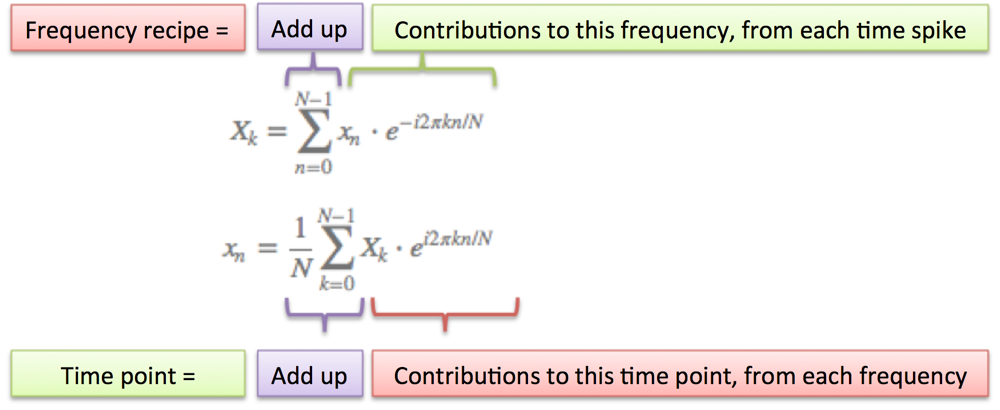
几点注意事项:
- N = 我们拥有的时间样本数量
- n = 当前考虑的样本(0 ... N-1)
- xn = 时间 n 处信号的值
- k = 当前考虑的频率(0 Hertz 到 N-1 Hertz)
- Xk = 信号中频率 k 的量(振幅和相位,一个复数)
- 通常将1/N因子移到反向变换中(从频率回到时间)。虽然这样做是可以的,但我更喜欢在正向变换中使用1/N,因为它给出了时间尖峰的实际大小。你可以在两个变换上甚至使用1/sqrt(N)(向前和向后都会创建1/N因子)。
- n/N 是我们已经经历的时间百分比。2 _ pi _ k 是我们的速度(弧度/秒)。e^-ix 是我们向后移动的圆形路径。组合是我们已经移动的距离,以这个速度和时间。
- 原始傅里叶变换的方程只是说“加复数”。许多编程语言不能直接处理复数,所以你需要将所有东西转换为直角坐标并相加那些。
斯图尔特·里夫对傅里叶变换有很好的解释:
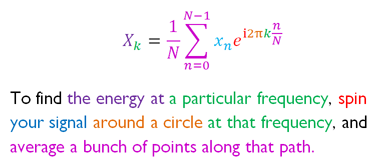
参考资料