N-皇后问题

八皇后问题是在一个8×8的国际象棋棋盘上放置八枚国际象棋皇后，使得任意两个皇后都不能互相攻击。因此，解决方案要求没有任何两个皇后位于同一行、列或对角线上。八皇后问题是更一般的n皇后问题的一个特例，在一个n×n的国际象棋棋盘上放置n个非攻击性皇后，对于所有自然数n都有解，除了n=2和n=3。

例如，下面是一个4皇后问题的解决方案。

N皇后

预期的输出是一个二进制矩阵，其中放置皇后的块用1表示。例如，上面4皇后解决方案的输出矩阵如下：

{ 0,  1,  0,  0}
{ 0,  0,  0,  1}
{ 1,  0,  0,  0}
{ 0,  0,  1,  0}

朴素算法

生成棋盘上所有可能的皇后配置，并打印满足给定约束的配置。

当还有未尝试的配置时
{
   生成下一个配置
   如果在这个配置中没有皇后冲突，则
   {
      打印这个配置；
   }
}

回溯算法

这个想法是从最左边的列开始，逐列放置皇后。当我们在一个列中放置一个皇后时，我们会检查与已放置的皇后是否有冲突。在当前列中，如果我们找到一个没有冲突的行，我们将标记这个行和列为解决方案的一部分。如果没有找到这样的行，由于冲突，我们将回溯并返回false。

1) 从最左列开始
2) 如果所有皇后都已放置
    返回true
3) 尝试当前列的所有行。 对于每个尝试的行：
    a) 如果在这个行中可以安全地放置皇后，则将这个[row, column]标记为解决方案的一部分，并递归检查在这里放置皇后是否会导致解决方案。
    b) 如果在[row, column]放置皇后会导致解决方案，则返回true。
    c) 如果在[row, column]放置皇后不会导致解决方案，则取消标记这个[row, column]（回溯）并转到步骤(a)尝试其他行。
3) 如果所有行都已尝试并且没有工作成果，则返回false以触发回溯。

位运算解决方案

位运算算法基本上是这样解决问题的：

皇后可以水平、垂直或对角线攻击。因此，每一行只能有一个皇后，每一列也只能有一个皇后，每个对角线上最多只能有一个皇后。
由于我们知道每一行只能有一个皇后，我们将从第一行开始，放置一个皇后，然后移动到第二行，放置第二个皇后，依此类推，直到 a) 我们达到一个有效的解决方案，或者 b) 我们到达一个死胡同（即我们不能放置一个皇后，使其免受其他皇后的攻击）。
由于我们每次只放置一行皇后，我们不需要担心水平攻击，因为不会有皇后位于同一行上的另一个皇后。
这意味着我们只需要在放置某个方格的皇后之前检查三件事情：1) 该方格的列上没有其他皇后，2) 该方格的左对角线上没有其他皇后，以及3) 该方格的右对角线上没有其他皇后。
如果我们最终到达一个无法安全放置皇后的地方，我们可以放弃当前的尝试，并立即测试下一个可能性。

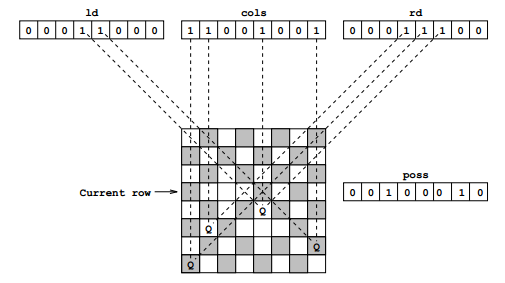
首先让我们谈谈递归函数。你会发现它接受3个参数：leftDiagonal、column和rightDiagonal。这些参数在技术上都是整数，但算法利用了一个事实，即一个整数由一系列位表示。所以，将这些参数视为N位的序列。

每个参数中的每个位代表当前行上相应位置是否“可用”。

例如： - 对于N=4，列值为0010将意味着第三列已经被一个皇后占据。 - 对于N=8，在第5行的ld值为00011000将意味着通过该行的第4和第5列的从左上到右下的对角线已经有了皇后。

下面是leftDiagonal、column和rightDiagonal的视觉辅助。

leftDiagonal

N-皇后问题

朴素算法

回溯算法

位运算解决方案

参考资料