雨水滞留问题(捕获雨水)
给定一个表示地形图中台阶高度的非负整数数组,其中每个台阶的宽度为1,计算雨后它能捕获多少雨水。
示例
示例 #1
输入:arr[] = [2, 0, 2]
输出:2
结构如下所示:
| |
|_|
我们可以在中间间隙捕获2个单位的雨水。
示例 #2
输入:arr[] = [3, 0, 0, 2, 0, 4]
输出:10
结构如下所示:
|
| |
| | |
|__|_|
我们可以在3和2之间捕获“3*2个单位”的雨水,在2上面捕获“1个单位”,在2和4之间捕获“3个单位”。也可以参见下面的图表。
示例 #3
输入:arr[] = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
输出:6
结构如下所示:
|
| || |
_|_||_||||||
在第一个1和第二个1之间捕获“1个单位”的雨水,在最后一个1和倒数第二个2之间捕获“4个单位”的雨水。
算法
如果一个元素左边和右边都有更高的台阶,则该元素可以存储水。我们可以通过找到左边和右边台阶的最大高度来计算每个元素可以存储的水量。例如,考虑数组[3, 0, 0, 2, 0, 4],我们可以捕获“3*2个单位”的雨水在3和2之间,“1个单位”在2上面和“3个单位”在2和4之间。也可以参见下面的图表。
方法1:暴力破解
直觉
对于数组中的每个元素,我们找到它雨后能捕获的最大水量,这等于两边最大高度的最小值减去它自己的高度。
步骤
- 初始化
answer = 0 - 从左到右遍历数组:
- 初始化
max_left = 0和max_right = 0 - 从当前元素开始到数组开头更新:
max_left = max(max_left, height[j]) - 从当前元素开始到数组结尾更新:
max_right = max(max_right, height[j]) - 将
min(max_left, max_right) − height[i]添加到answer
复杂度分析
时间复杂度:O(n^2)。对于数组中的每个元素,我们遍历左右两侧各一次。
辅助空间复杂度:O(1)的额外空间。
方法2:动态规划
直觉
在暴力破解中,我们再次反复遍历左右两侧,只是为了找到该索引之前的最高台阶大小。但是,这个值可以被存储起来。看吧,这就是动态规划。
因此,我们可以在O(n)时间内预计算出每个台阶左右两侧的最高台阶。然后使用这些预计算出的值来找到数组中每个元素的水量。
该概念如图所示:
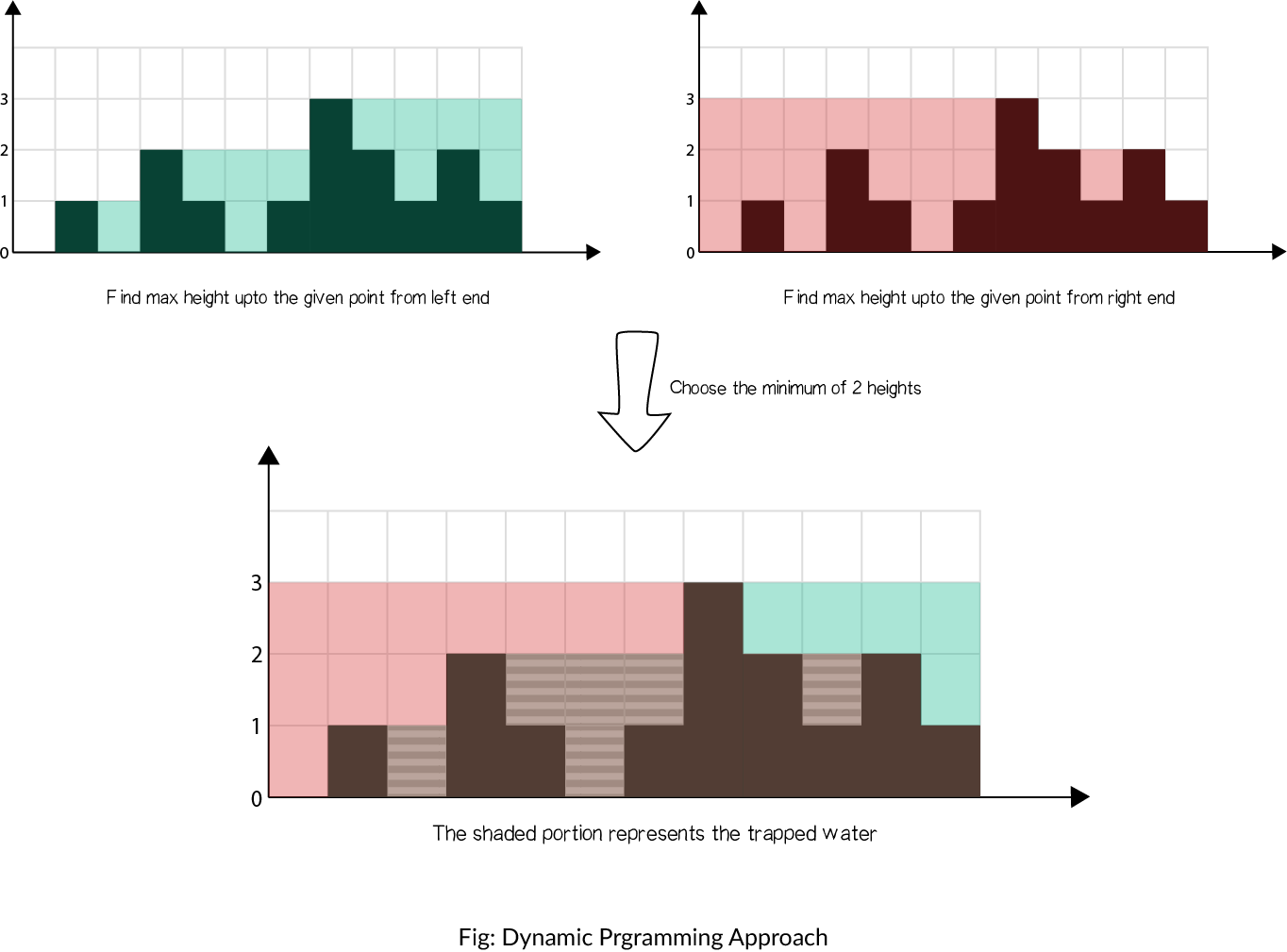
步骤
- 在数组的第
i个位置之前,找到从左边开始的最高台阶left_max[i]。 - 在数组的第
i个位置之前,找到从右边开始的最高台阶right_max[i]。 - 遍历
height数组并更新answer: - 将
min(max_left[i], max_right[i]) − height[i]添加到answer。
复杂度分析
时间复杂度:O(n)。我们使用两次O(n)的时间迭代来存储最多高度,最后使用存储的值更新answer。
辅助空间复杂度:O(n)的额外空间。比方法1多了left_max和right_max数组的额外空间。