JavaScript 알고리즘 및 자료 구조

이 저장소에는 많이 알려진 알고리즘 및 자료 구조의 Javascript 기반 예제를 담고 있습니다.

각 알고리즘과 자료 구조에 대해 연관되어 있는 설명이 README에 작성되어 있으며, 링크를 통해 더 자세한 설명을 만날 수 있습니다. (관련된 YouTube 영상도 포함).

Read this in other languages: English, 简体中文, 繁體中文, 日本語, Polski, Français, Español, Português, Русский, Türk, Italiana, Bahasa Indonesia, Українська, Arabic, Tiếng Việt, Deutsch, Uzbek

자료 구조

자료 구조는 데이터를 특정 방식으로 구성하고 저장함으로써 더 효율적으로 접근하고 수정할 수 있게 해줍니다. 간단히 말해, 자료 구조는 데이터 값들, 데이터 간의 관계, 그리고 데이터를 다룰 수 있는 함수와 작업의 모임입니다.

B - 입문자, A - 숙련자

B 연결 리스트
B 이중 연결 리스트
B 큐
B 스택
B 해시 테이블
B 힙
B 우선순위 큐
A 트라이
A 트리
A 이진 탐색 트리
A AVL 트리
A Red-Black 트리
A 세그먼트 트리 - min/max/sum range 쿼리 예제.
A Fenwick 트리 (Binary Indexed Tree)
A 그래프 (유방향, 무방향)
A 서로소 집합
A 블룸 필터

알고리즘

알고리즘은 어떤 종류의 문제를 풀 수 있는 정확한 방법이며, 일련의 작업을 정확하게 정의해 놓은 규칙들입니다.

B - 입문자, A - 숙련자

주제별 알고리즘

Math
B Bit Manipulation - set/get/update/clear bits, 2의 곱 / 나누기, 음수로 만들기 etc.
B 팩토리얼
B 피보나치 수
B 소수 판별 (trial division 방식)
B 유클리드 호제법 - 최대공약수 (GCD)
B 최소 공배수 - LCM
B 에라토스테네스의 체 - 특정수 이하의 모든 소수 찾기
B 2의 거듭제곱 판별법 - 어떤 수가 2의 거듭제곱인지 판별 (naive 와 bitwise 알고리즘)
B 파스칼 삼각형
A 자연수 분할
A 리우 후이 π 알고리즘 - N-각형을 기반으로 π 근사치 구하기
Sets
B 카티지언 프로덕트 - 곱집합
B Fisher–Yates 셔플 - 유한 시퀀스의 무작위 순열
A 멱집합 - 집합의 모든 부분집합
A 순열 (반복 유,무)
A 조합 (반복 유,무)
A 최장 공통 부분수열 (LCS)
A 최장 증가 수열
A Shortest Common Supersequence (SCS)
A 배낭 문제 - "0/1" 과 "Unbound"
A 최대 구간합 - "브루트 포스" 과 "동적 계획법" (Kadane's) 버전
A 조합 합 - 특정 합을 구성하는 모든 조합 찾기
Strings
B 해밍 거리 - 심볼이 다른 위치의 갯수
A 편집 거리 - 두 시퀀스 간위 최소 편집거리
A 커누스-모리스-프랫 알고리즘 (KMP 알고리즘) - 부분 문자열 탐색 (패턴 매칭)
A Z 알고리즘 - 부분 문자열 탐색 (패턴 매칭)
A 라빈 카프 알고리즘 - 부분 문자열 탐색
A 최장 공통 부분 문자열
A 정규 표현식 매칭
Searches
B 선형 탐색
B 점프 탐색 (or Block Search) - 정렬된 배열에서 탐색
B 이진 탐색 - 정렬된 배열에서 탐색
B 보간 탐색 - 균등한 분포를 이루는 정렬된 배열에서 탐색
Sorting
B 거품 정렬
B 선택 정렬
B 삽입 정렬
B 힙 정렬
B 병합 정렬
B 퀵 정렬 - 제자리(in-place)와 제자리가 아닌(non-in-place) 구현
B 셸 정렬
B 계수 정렬
B 기수 정렬
Trees
B 깊이 우선 탐색 (DFS)
B 너비 우선 탐색 (BFS)
Graphs
B 깊이 우선 탐색 (DFS)
B 너비 우선 탐색 (BFS)
B 크루스칼 알고리즘 - 최소 신장 트리 찾기 (MST) 무방향 가중 그래프
A 다익스트라 알고리즘 - 한 점에서 다른 모든 점까지 최단 거리 찾기
A 벨만-포드 알고리즘 - 한 점에서 다른 모든 점까지 최단 거리 찾기
A 플로이드-워셜 알고리즘 - 모든 종단 간의 최단거리 찾기
A 사이클 탐지 - 유방향, 무방향 그래프 (DFS 와 Disjoint Set 에 기반한 버전)
A 프림 알고리즘 - 무방향 가중치 그래프에서 최소 신장 트리 (MST) 찾기
A 위상 정렬 - DFS 방식
A 단절점 - 타잔의 알고리즘 (DFS 기반)
A 단절선 - DFS 기반 알고리즘
A 오일러 경로 와 오일러 회로 - Fleury의 알고리즘 - 모든 엣지를 한번만 방문
A 해밀턴 경로 - 모든 꼭짓점을 한번만 방문
A 강결합 컴포넌트 - Kosaraju의 알고리즘
A 외판원 문제 - 각 도시를 다 방문하고 다시 출발점으로 돌아오는 최단 경로 찾기
Uncategorized
B 하노이 탑
B 정방 행렬 회전 - 제자리(in-place) 알고리즘
B 점프 게임 - 백트래킹, 동적계획법 (top-down + bottom-up), 탐욕 알고리즘 예제
B Unique 경로 - 백트래킹, 동적계획법, 파스칼 삼각형에 기반한 예제
B 빗물 담기 문제 - trapping rain water problem (동적계획법, 브루트포스 버전)
A N-Queens 문제
A 기사의 여행 문제

패러다임별 알고리즘

알고리즘 패러다임 이란, 알고리즘이 주어진 문제를 해결하기 위해 채택한 기초가 되는 일반적인 방법 혹은 접근법입니다. 알고리즘이 해결하는 문제나 알고리즘의 동작 방식이 완전히 다르더라도,알고리즘의 동작 원칙이 같으면 같은 패러다음을 사용했다고 말할 수 있으며, 주로 알고리즘을 구분하는 기준으로 쓰인다. 알고리즘이 일반적인 컴퓨터의 프로그램에 대한 개념보다 보다 더 추상적인 개념인 것처럼 알고리즘의 패러다임은 명확히 정의된 수학적 실체가 있는 것이 아니기 때문에 그 어떤 알고리즘의 개념보다도 훨씬 추상적인 개념입니다.

브루트 포스(Brute Force) - 가능한 모든 경우를 탐색한 뒤 최적을 찾아내는 방식입니다.
B 선형 탐색
B 빗물 담기 문제 - trapping rain water problem
A 최대 구간합
A 외판원 문제 - 각 도시를 다 방문하고 다시 출발점으로 돌아오는 최단 경로 찾기
탐욕 알고리즘(Greedy) - 이후를 고려하지 않고 현재 시점에서 가장 최적인 선택을 하는 방식입니다.
B 점프 게임
A 쪼갤수 있는 배낭 문제
A 다익스트라 알고리즘 - 모든 점 까지의 최단거리 찾기
A 프림 알고리즘 - 무방향 가중치 그래프에서 최소 신창 트리 (MST) 찾기
A 크루스칼 알고리즘 - 무방향 가중치 그래프에서 최소 신창 트리 (MST) 찾기
분할 정복법(Divide and Conquer) - 문제를 여러 작은 문제로 분할한 뒤 해결하는 방식입니다.
B 이진 탐색
B 하노이 탑
B 파스칼 삼각형
B 유클리드 호제법 - 최대공약수 계산 (GCD)
B 병합 정렬
B 퀵 정렬
B 트리 깊이 우선 탐색 (DFS)
B 그래프 깊이 우선 탐색 (DFS)
B 점프 게임
A 순열 (반복 유,무)
A 조합 (반복 유,무)
동적 계획법(Dynamic Programming) - 이전에 찾은 결과를 이용하여 최종적으로 해결하는 방식입니다.
B 피보나치 수
B 점프 게임
B Unique Paths
B 빗물 담기 문제 - trapping rain water problem
A 편집 거리 - 두 시퀀스 간의 최소 편집 거리
A 최장 공통 부분 수열 (LCS)
A 최장 공통 부분 문자열
A 최장 증가 수열
A Shortest Common Supersequence
A 0/1 배낭 문제
A 자연수 분할
A 최대 구간합
A 벨만-포드 알고리즘 - 모든 점 까지의 최단 거리 찾기
A 플로이드-워셜 알고리즘 - 모든 종단 간의 최단거리 찾기
A 정규 표현식 매칭
백트래킹(Backtracking) - 모든 가능한 경우를 고려한다는 점에서 브루트 포스와 유사합니다. 하지만 다음 단계로 넘어갈때 마다 모든 조건을 만족했는지 확인하고 진행합니다. 만약 조건을 만족하지 못했다면 뒤로 돌아갑니다 (백트래킹). 그리고 다른 경로를 선택합니다. 보통 상태를 유지한 DFS 탐색을 많이 사용합니다.
B 점프 게임
B Unique Paths
A 해밀턴 경로 - 모든 점을 한번씩 방문
A N-Queens 문제
A 기사의 여행
A 조합 합 - 특정 합을 구성하는 모든 조합 찾기
분기 한정법 - 백트래킹으로 찾은 각 단계의 최소 비용이 드는 해를 기억해 두고 있다가, 이 비용을 이용해서 더 낮은 최적의 해를 찾습니다. 기억해둔 최소 비용들을 이용해 더 높은 비용이 드는 해결법을 탐색 안함으로써 불필요한 시간 소모를 줄입니다. 보통 상태 공간 트리의 DFS 탐색을 이용한 BFS 탐색 방식에서 사용됩니다.

이 저장소의 사용법

모든 종속 모듈들 설치

npm install

ESLint 실행

코드의 품질을 확인 할 수 있습니다.

npm run lint

모든 테스트 실행

npm test

이름을 통해 특정 테스트 실행

npm test -- 'LinkedList'

Playground

./src/playground/playground.js 파일을 통해 자료 구조와 알고리즘을 작성하고 ./src/playground/__test__/playground.test.js에 테스트를 작성할 수 있습니다.

그리고 간단하게 아래 명령어를 통해 의도한대로 동작하는지 확인 할 수 있습니다.:

npm test -- 'playground'

유용한 정보

참고

▶ Data Structures and Algorithms on YouTube

Big O 표기

Big O 표기로 표시한 알고리즘의 증가 양상입니다.

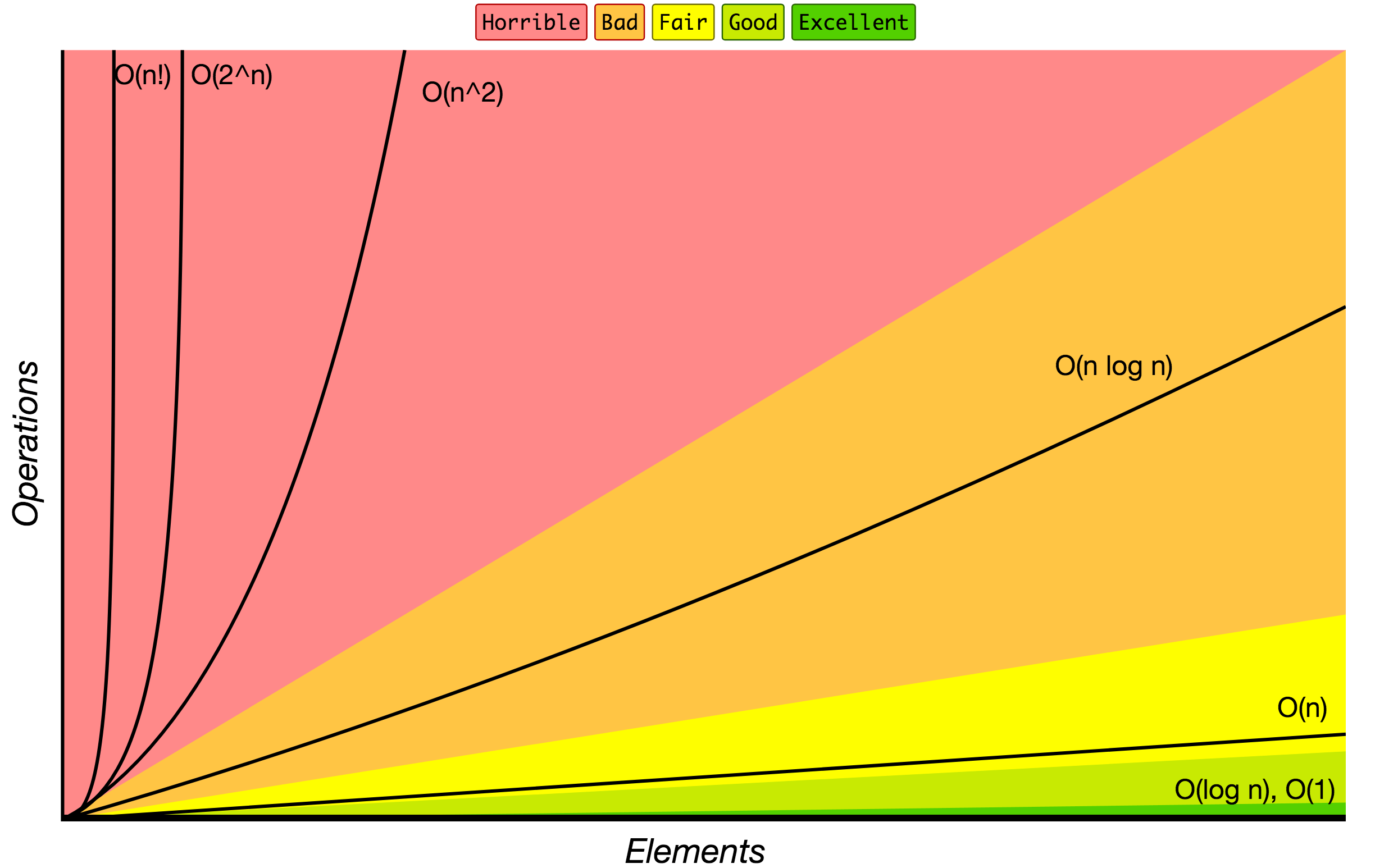
Big O graphs

Source: Big O Cheat Sheet.

아래는 가장 많이 사용되는 Big O 표기와 입력 데이터 크기에 따른 성능을 비교한 표입니다.

Big O 표기	10 개 일때	100 개 일때	1000 개 일때
O(1)	1	1	1
O(log N)	3	6	9
O(N)	10	100	1000
O(N log N)	30	600	9000
O(N^2)	100	10000	1000000
O(2^N)	1024	1.26e+29	1.07e+301
O(N!)	3628800	9.3e+157	4.02e+2567

자료 구조 작업별 복잡도

자료 구조	접근	검색	삽입	삭제	비고
배열	1	n	n	n
스택	n	n	1	1
큐	n	n	1	1
연결 리스트	n	n	1	1
해시 테이블	-	n	n	n	완벽한 해시 함수의 경우 O(1)
이진 탐색 트리	n	n	n	n	균형 트리의 경우 O(log(n))
B-트리	log(n)	log(n)	log(n)	log(n)
Red-Black 트리	log(n)	log(n)	log(n)	log(n)
AVL 트리	log(n)	log(n)	log(n)	log(n)
Bloom Filter	-	1	1	-	거짓 양성이 탐색 중 발생 가능

정렬 알고리즘 복잡도

이름	최적	평균	최악	메모리	동일값 순서유지	비고
거품 정렬	n	n²	n²	1	Yes
삽입 정렬	n	n²	n²	1	Yes
선택 정렬	n²	n²	n²	1	No
힙 정렬	n log(n)	n log(n)	n log(n)	1	No
병합 정렬	n log(n)	n log(n)	n log(n)	n	Yes
퀵 정렬	n log(n)	n log(n)	n²	log(n)	No	퀵 정렬은 보통 제자리(in-place)로 O(log(n)) 스택공간으로 수행됩니다.
셸 정렬	n log(n)	간격 순서에 영향을 받습니다.	n (log(n))²	1	No
계수 정렬	n + r	n + r	n + r	n + r	Yes	r - 배열내 가장 큰 수
기수 정렬	n * k	n * k	n * k	n + k	Yes	k - 키값의 최대 길이

ℹ️ A few more projects and articles about JavaScript and algorithms on trekhleb.dev