内容感知的图像调整在JavaScript中

这里有一个互动版本的这篇文章,你可以上传并调整你自己的图片。
简洁回顾
关于缝切割算法的文章已经有很多了,但我不禁想要自己探索这个优雅、强大且简单的算法,并分享我的个人体验。另一个引起我注意的点是,动态规划(DP)方法可能被平滑地应用于解决这个问题。如果你像我一样,还在学习算法的旅程中,这个算法解决方案可能会丰富你的个人DP武器库。
所以,有了这篇文章,我想做三件事:
- 提供一个互动式的内容感知调整器,这样你可以随意调整你自己的图片大小
- 解释缝切割算法背后的思想
- 解释实现该算法的动态规划方法(我们将使用TypeScript来实现它)
内容感知的图像调整
内容感知的图像调整可能在改变图像比例(即减少宽度同时保持高度)时应用,或者在丢失图像的部分不是理想的情况下应用。在这种情况下,直接对图像进行缩放会扭曲其中的对象。为了在改变图像比例的同时保留对象的原始比例,我们可以使用缝切割算法,由Shai Avidan和Ariel Shamir引入。
下面的示例显示了如何使用内容感知调整将原始图像的宽度减少了50%(左图)和直接缩放(右图)。在这个特定的例子中,左图看起来更自然,因为气球的比例得到了保留。

缝切割算法的思想是找到对图像内容贡献最低的缝隙(连续的像素序列),然后切割(移除)它。这个过程会一遍又一遍地重复,直到我们得到所需的图像宽度或高度。在下面的示例中,你可能会看到热气球像素对图像内容的贡献比天空像素更多。因此,天空像素首先被移除。

找到能量最低的缝隙是一个计算成本高昂的任务(尤其是对于大图像)。为了使缝隙搜索更快,可能应用动态规划方法(我们将在下面详细讨论实现细节)。
对象移除
每个像素的重要性(所谓的像素能量)是基于其颜色(R、G、B、A)与其相邻像素之间的差异来计算的。现在,如果我们人为地将像素能量设置得很低(即在它们上面绘制掩码),那么缝切割算法将为我们免费执行对象移除。

JS图像切割器演示
我创建了JS图像切割器网页应用(并在GitHub上开源),你可以使用它来尝试调整你自己的图片大小。
更多示例
这里有一些更多的示例,展示了算法如何处理更复杂的背景。
山脉背景被平滑地缩小,没有明显的缝隙。

海洋波浪也是如此。算法保留了波浪结构,而没有扭曲冲浪者。

我们需要记住,缝切割算法并不是万能的,如果大部分像素都是边缘(对算法来说很重要),它可能无法正确调整图像。在这种情况下,它甚至开始扭曲图像中重要的部分。在下面的示例中,内容感知的图像调整看起来与直接缩放非常相似,因为对算法来说所有像素看起来都很重要,很难区分梵高的脸和背景。

缝切割算法的工作原理
想象我们有一个1000 x 500 px的照片,我们想将其大小调整为500 x 500 px以使其成为正方形(假设正方形的比率更适合Instagram的布局)。在这种情况下,我们可能需要为调整过程设定几个要求:
- 保留图像的重要部分(也就是说,如果之前有5棵树,我们希望在调整后仍然有5棵树)。
- 保留图像重要部分的比例(例如,圆形车轮不应被挤压成椭圆形车轮) 为避免更改图像的重要部分,我们可能会找到从上到下连续的像素序列(接缝),它对图像内容的贡献最低(避开重要部分),然后将其移除。移除接缝会使图像缩小1个像素。然后我们将重复此步骤,直到图像达到所需的宽度。
问题是如何定义像素的重要性及其对内容的贡献(在原始论文中,作者使用术语像素的能量)。实现这一目标的方法之一是将构成边缘的所有像素视为重要像素。如果一个像素是边缘的一部分,它的颜色与其邻居(左边的像素和右边的像素)之间的差异会比非边缘像素更大。
![]()
假设一个像素的颜色由4个数字表示(R - 红色,G - 绿色,B - 蓝色,A - 透明度),我们可以使用以下公式来计算颜色差异(像素能量):
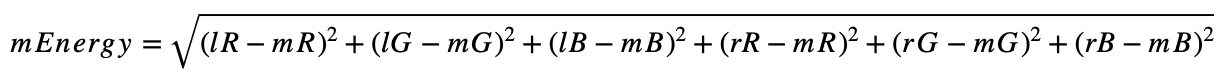
其中:
mEnergy- 中间像素的能量(重要性)(如果四舍五入,则为[0..626])lR- 左边像素的红色通道值([0..255])mR- 中间像素的红色通道值([0..255])rR- 右边像素的红色通道值([0..255])lG- 左边像素的绿色通道值([0..255])- 等等...
在上述公式中,我们暂时省略了透明度(透明度)通道,假设图像中没有透明像素。稍后我们将使用透明度通道进行遮罩和物体移除。
![]()
现在,既然我们知道如何找到一个像素的能量,我们可以计算所谓的能量图,这将包含图像每个像素的能量。在每次调整大小时,都应该重新计算能量图(至少部分地,下面会详细介绍),并且其大小将与图像相同。
例如,在第一次调整大小时,我们将有一个1000 x 500的图像和一个1000 x 500的能量图。在第二次调整大小时,我们将从图像中移除接缝,并根据新的缩小后的图像重新计算能量图。因此,我们将得到一个999 x 500的图像和一个999 x 500的能量图。
像素的能量越高,它就越可能是边缘的一部分,这对于图像内容和减少需要移除的可能性都很重要。
为了可视化能量图,我们可以将较亮的颜色分配给能量较高的像素,将较暗的颜色分配给能量较低的像素。这里是一个人工示例,展示了能量图的随机部分可能看起来如何。您可能会看到代表边缘的明亮线条,我们希望在调整大小过程中保留它。
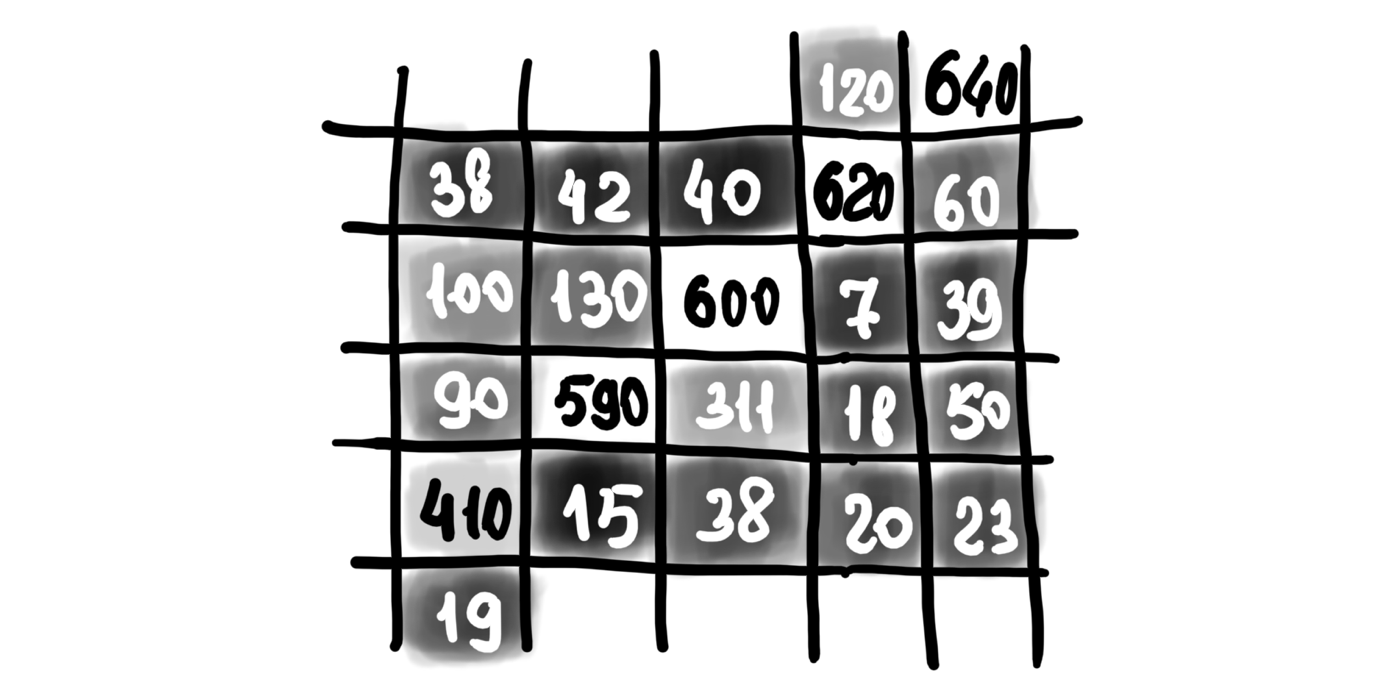
这是您上面看到的演示图像的能量图的真实示例(带有热气球)。

您可以尝试自定义图像,并查看在互动版本的帖子中的能量图会是什么样子。
我们可以使用能量图来找到一系列能量最低的接缝,并通过这样做来决定哪些像素最终应该被删除。
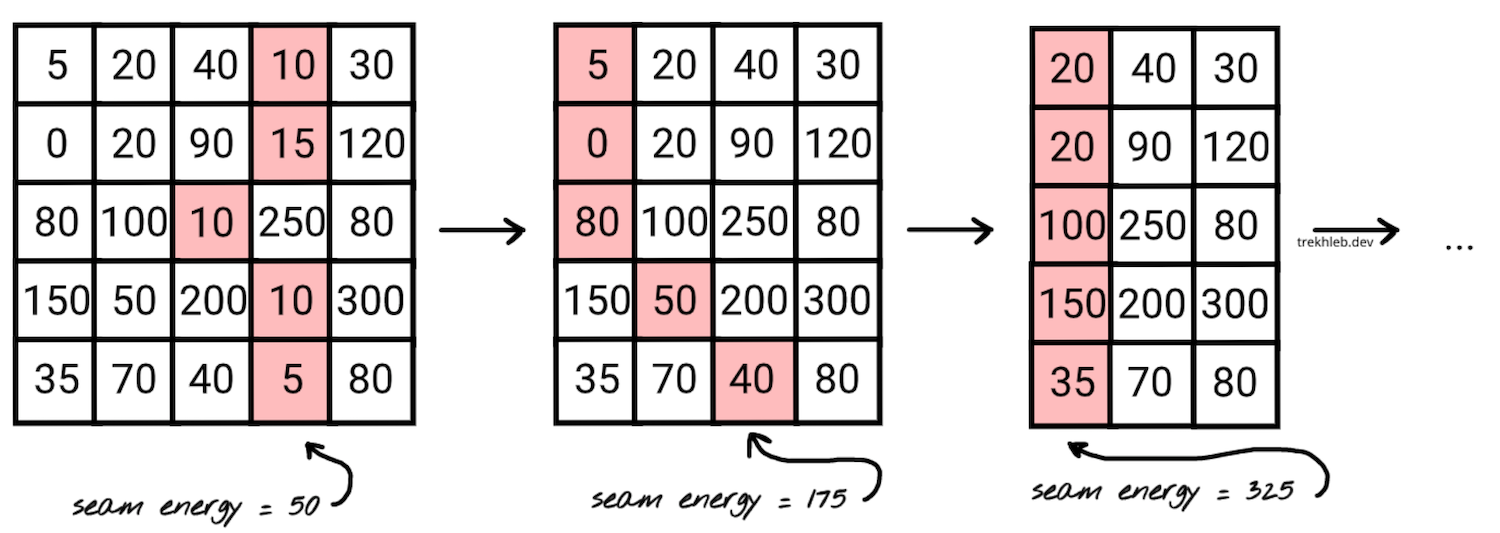
找到能量最低的接缝并非易事,需要在做出决策之前探索许多可能的像素组合。我们将采用动态规划方法来加速这一过程。
在下面的示例中,您可能会看到找到了第一个最低能量的接缝的能量图。

在上述示例中,我们正在减少图像的宽度。采取类似的方法也可以减少图像的高度。不过,我们需要“旋转”这种方法:
- 开始使用顶部和底部像素邻居(而不是左侧和右侧)来计算像素能量
- 在搜索接缝时,我们需要从左侧移动到右侧(而不是从上部移动到下部)
TypeScript 实现
您可以在js-image-carver仓库中找到源代码以及下面提到的函数。
要实现算法,我们将使用TypeScript。如果您想要JavaScript版本,您可以忽略(删除)类型定义及其用法。
出于简单原因,让我们只实现图像宽度缩减的接缝雕刻算法。
内容感知宽度调整(入口函数)
首先,让我们定义一些在实现算法时将要使用的常见类型。
// 描述图像尺寸(宽度和高度)的类型。
type ImageSize = { w: number, h: number };
// 像素的坐标。
type Coordinate = { x: number, y: number };
// 接缝是一系列像素(坐标)。
类型 Seam = 坐标[];
// 能量图是一个与图像计算时相同的宽度和高度的二维数组。
类型 EnergyMap = 数字[][];
// 描述图像像素的 RGBA 颜色的类型。
类型 Color = [
r: 数字, // 红色
g: 数字, // 绿色
b: 数字, // 蓝色
a: 数字, // 透明度(透明)
] | Uint8ClampedArray;
算法的高层主要包括以下步骤:
1. 计算当前版本图像的 **能量图**。
2. 根据能量图找到具有最低能量的 **接缝**(我们将在此应用动态规划)。
3. **删除** 具有最低能量接缝的图像中的接缝。
4. **重复** 直到图像宽度减小到所需的值。
```typescript
类型 ResizeImageWidthArgs = {
img: ImageData, // 我们想要调整大小的图像数据。
toWidth: 数字, // 我们希望图像缩小的最终宽度。
};
类型 ResizeImageWidthResult = {
img: ImageData, // 调整大小后的图像数据。
size: ImageSize, // 调整大小后的图像尺寸(宽 x 高)。
};
// 使用接缝雕刻方法执行内容感知的图像宽度调整。
export const resizeImageWidth = (
{ img, toWidth }: ResizeImageWidthArgs,
): ResizeImageWidthResult => {
// 出于性能原因,我们不想改变 img 数据数组的大小。
// 取而代之的是,我们只需分别记录调整大小后的图像宽度和高度。
const size: ImageSize = { w: img.width, h: img.height };
// 计算需要移除的像素数量。
const pxToRemove = img.width - toWidth;
if (pxToRemove < 0) {
throw new Error('缩放目前不支持');
}
let energyMap: EnergyMap | null = null;
let seam: Seam | null = null;
// 逐个删除最低能量的接缝。
for (let i = 0; i < pxToRemove; i += 1) {
// 1. 计算当前版本图像的能量图。
energyMap = calculateEnergyMap(img, size);
// 2. 根据能量图找到具有最低能量的接缝。
seam = findLowEnergySeam(energyMap, size);
// 3. 删除图像中具有最低能量的接缝。
deleteSeam(img, seam, size);
// 缩小图像宽度,并继续迭代。
size.w -= 1;
}
// 返回调整大小后的图像及其最终大小。
// img 实际上是对 ImageData 的引用,所以从技术上讲,
// 函数调用者已经拥有这个指针。但为了更好的代码可读性,
// 我们还是返回它。
return { img, size };
};
需要调整大小的图像以 ImageData 格式传递给函数。您可以在画布上绘制图像,然后像这样从画布中提取 ImageData:
const ctx = canvas.getContext('2d');
const imgData = ctx.getImageData(0, 0, imgWidth, imgHeight);
在本文的范围内,JavaScript 中上传和绘制图像的方法不在讨论范围内,但您可以在 js-image-carver 仓库中找到使用 React 完成此操作的完整源代码。
让我们将每个步骤分解并逐一实现 calculateEnergyMap(), findLowEnergySeam() 和 deleteSeam() 函数。
计算像素的能量
这里我们应用上述颜色差异公式。对于左边界和右边界(当没有左右邻居时),我们忽略邻居,在能量计算过程中不考虑它们。
// 计算像素的能量。
const getPixelEnergy = (left: Color | null, middle: Color, right: Color | null): number => {
// 中间像素是我们计算能量的像素。
const [mR, mG, mB] = middle;
// 左像素的能量(如果存在)。
let lEnergy = 0;
if (left) {
const [lR, lG, lB] = left;
lEnergy = (lR - mR) ** 2 + (lG - mG) ** 2 + (lB - mB) ** 2;
}
// 右像素的能量(如果存在)。
let rEnergy = 0;
if (right) {
const [rR, rG, rB] = right;
rEnergy = (rR - mR) ** 2 + (rG - mG) ** 2 + (rB - mB) ** 2;
}
// 结果像素的能量。
return Math.sqrt(lEnergy + rEnergy);
};
计算能量图
我们正在处理的图像具有 ImageData 格式。这意味着所有像素(及其颜色)都存储在一个平坦的(1D)Uint8ClampedArray数组中。为了可读性目的,让我们引入两个帮助函数,这些函数将允许我们使用 Uint8ClampedArray 数组作为 2D 矩阵工作。
// 辅助函数,返回像素的颜色。
const getPixel = (img: ImageData, { x, y }: Coordinate): Color => {
// ImageData 数据数组是一个平坦的 1D 数组。
// 因此我们需要将 x 和 y 坐标转换为线性索引。
const i = y * img.width + x;
const cellsPerColor = 4; // RGBA
// 为了提高效率,我们不是创建一个新的子数组,而是返回
// ImageData 数组的一部分的指针。
return img.data.subarray(i * cellsPerColor, i * cellsPerColor + cellsPerColor);
};
// 辅助函数,设置像素的颜色。
const setPixel = (img: ImageData, { x, y }: Coordinate, color: Color): void => {
// ImageData 数据数组是一个平坦的 1D 数组。
// 因此我们需要将 x 和 y 坐标转换为线性索引。
const i = y * img.width + x;
const cellsPerColor = 4; // RGBA
img.data.set(color, i * cellsPerColor);
};
为了计算能量图,我们遍历图像中的每个像素,并对每个像素调用前述的 getPixelEnergy() 函数。
// 辅助函数,创建一个特定大小(w x h)的矩阵(2D 数组)并将其用指定的值填充。
const matrix = <T>(w: number, h: number, filler: T): T[][] => {
return new Array(h)
.fill(null)
.map(() => {
return new Array(w).fill(filler);
```javascript
}; // 计算图像每个像素的能量。
const calculateEnergyMap = (img: ImageData, { w, h }: ImageSize): EnergyMap => {
// 创建一个空的能量图,其中每个像素都有无限高的能量。
// 我们将更新每个像素的能量。
const energyMap: number[][] = matrix<number>(w, h, Infinity);
for (let y = 0; y < h; y += 1) {
for (let x = 0; x < w; x += 1) {
// 如果我们在图像的左边缘,左侧像素可能不存在。
const left = (x - 1) >= 0 ? getPixel(img, { x: x - 1, y }) : null;
// 我们正在计算能量的中间像素的颜色。
const middle = getPixel(img, { x, y });
// 如果我们在图像的右边缘,右侧像素可能不存在。
const right = (x + 1) < w ? getPixel(img, { x: x + 1, y }) : null;
energyMap[y][x] = getPixelEnergy(left, middle, right);
}
}
return energyMap;
};
能量图将在每次调整大小时重新计算。这意味着,如果我们需要将图像缩小500像素,它将重新计算,比如说,500次,这并不是最佳选择。为了加快第2步、第3步及以后的能量图计算速度,我们可以只重新计算将要移除的接缝周围像素的能量。出于简化原因,这里省略了这种优化,但您可以在js-image-carver仓库中找到示例源代码。
以最低能量找到接缝(动态规划方法)
我之前在动态规划与分治文章中描述了一些动态规划基础知识。有一个基于最小编辑距离问题的DP示例。您可能会想查看它以获得一些更多的上下文。
我们现在需要解决的问题是找到从上到下、像素能量总和最小的能量图路径(接缝)。
假设的方法
假设的方法将是逐一检查所有可能的路径。
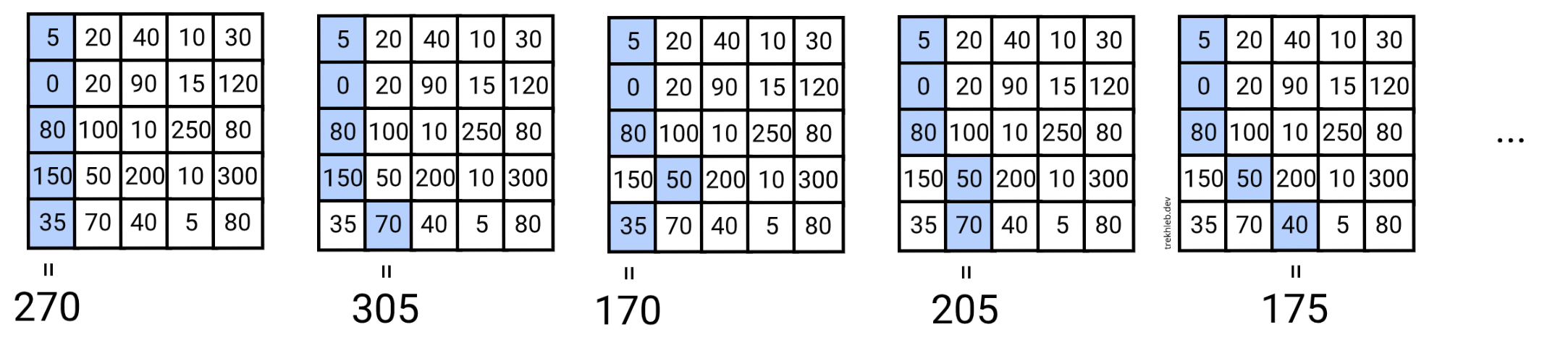
从上到下,对于每个像素,我们有3个选项(↙︎ 向左下移动,↓ 向下移动,↘︎ 向右下移动)。这给出了时间复杂度为O(w * 3^h)或简单地为O(3^h),其中w和h是图像的宽度和高度。这种方法看起来很慢。
贪婪方法
我们也可以尝试选择下一个像素作为能量最低的像素,希望得到的接缝能量是最小的。
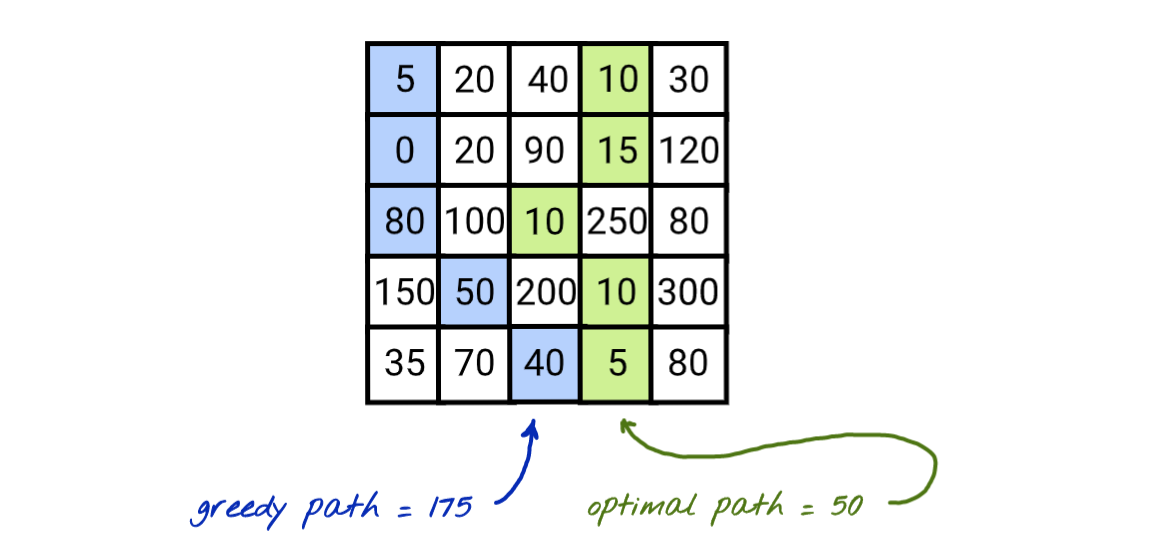
这种方法并不一定是最坏的解决方案,但它不能保证我们会找到最佳的可用解决方案。在上面的图像中,您可能会看到贪婪方法最初选择了5而不是10,并错过了最优像素链。
这种方法的好处是它速度快,时间复杂度为O(w + h),其中w和h是图像的宽度和高度。在这种情况下,速度的成本是小尺寸重绘的低质量。我们需要在第一行中找到最小值(遍历w个单元),然后我们只探索每行的3个相邻像素(遍历h行)。
动态规划方法
您可能已经注意到,在假设的方法中,我们在计算结果接缝的能量时一遍又一遍地累加了相同的像素能量。
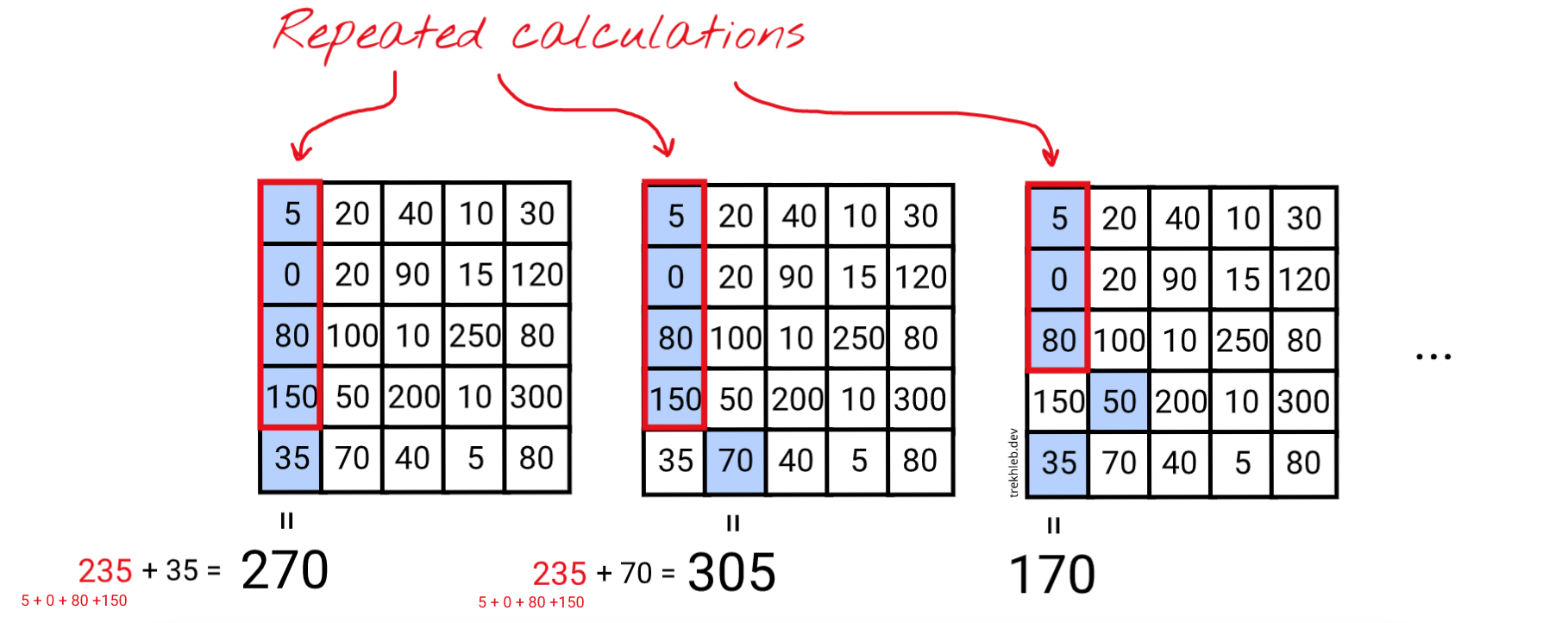
在上述示例中,您可以看到,对于前两个接缝,我们正在重用较短接缝的能量(其能量为235)。我们不是只做一个操作235 + 70来计算第2个接缝的能量,而是做了四个操作(5 + 0 + 80 + 150) + 70。
我们正在重用前一个接缝的能量来计算当前接缝的能量这一事实,可以递归地应用于所有更短的接缝,直到最顶部的第一行接缝。当我们有这样的重叠子问题时,这是一个迹象,表明一般问题可能可以通过动态规划方法进行优化。
因此,我们可以在额外的seamsEnergies表中存储当前接缝的特定像素的能量,以便更快地重新使用它来计算下一个接缝(seamsEnergies表的大小将与能量图和图像本身相同)。
还要记住,对于图像上的一个特定像素(即左下角的一个),我们可能有几个以前接缝的能量值。
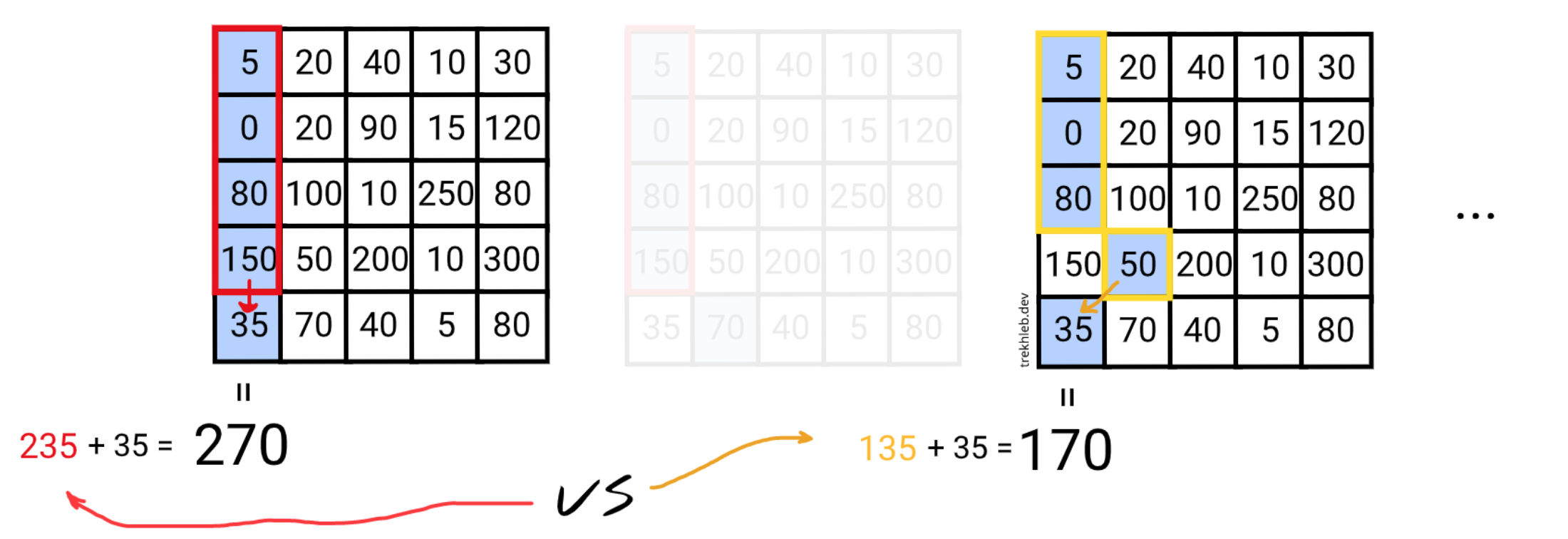
由于我们正在寻找具有最低结果能量的接缝,选择以前接缝中结果能量最低的接缝是有意义的。
一般来说,我们有三个可能的以前接缝可供选择:
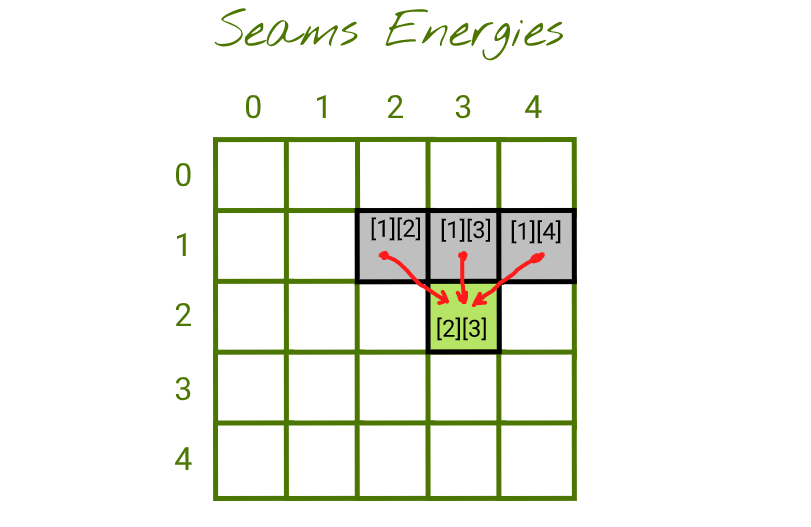
您可以这样考虑:
- 单元
[1][x]:包含从行[0][?]开始并在单元[1][x]结束的接缝的最低可能能量。 - 单元
[2][x]:包含从行[0][x+1]开始并在单元[2][x]结束的接缝的最低可能能量。 - 单元
[3][x]:包含从行[0][x+2]开始并在单元[3][x]结束的接缝的最低可能能量。 - 当前单元格
[2][3]:包含从行[0][?]上的某处开始并在单元格[2][3]结束的缝的最小可能能量。要计算它,我们需要将当前像素[2][3](来自能量图)的能量与min(seam_energy_1_2, seam_energy_1_3, seam_energy_1_4)相加。
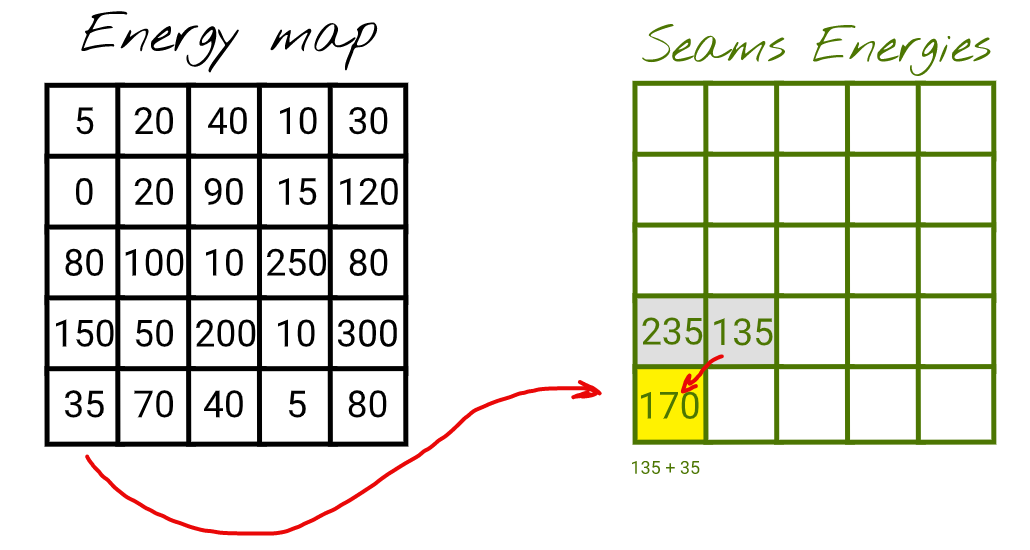
如果我们完全填充了 seamsEnergies 表格,那么最低行的最小值将是最低可能的缝能量。
让我们尝试填充这个表格的几个单元格来看看它是如何工作的。
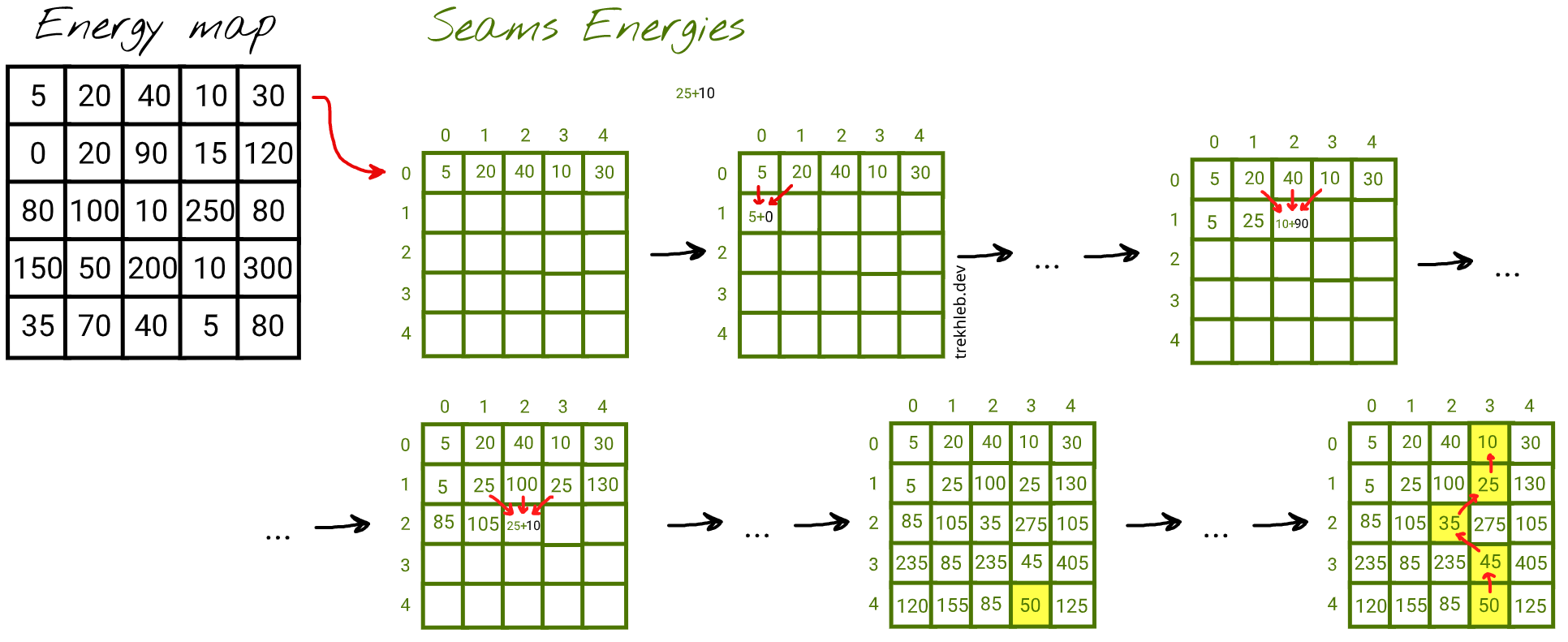
在填写完 seamsEnergies 表格后,我们可能会看到能量最低的像素具有 50 的能量。为了方便起见,在 seamsEnergies 生成过程中,我们可以不仅保存缝的能量,还可以保存前一个最低能量缝的坐标。这将使我们能够轻松地从底部到顶部重建缝路径。
动态规划方法的时间复杂度将是 O(w * h),其中 w 和 h 是图像的宽度和高度。我们需要为图像的每个像素计算能量。
这里是这种逻辑可能实现的一个例子:
// 奇缝像素的元数据。
type SeamPixelMeta = {
energy: number, // 像素的能量。
coordinate: Coordinate, // 像素的坐标。
previous: Coordinate | null, // 此时处于最低能量缝的前一个像素。
};
// 使用动态规划方法找到具有最低结果能量的缝(从上到下的像素序列)。
const findLowEnergySeam = (energyMap: EnergyMap, { w, h }: ImageSize): Seam => {
// 大小为 w 和 h 的 2D 数组,其中每个像素包含缝元数据(像素能量、像素坐标以及此时处于此点的最低能量缝的前一个像素)。
const seamsEnergies: (SeamPixelMeta | null)[][] = matrix<SeamPixelMeta | null>(w, h, null);
// 通过仅复制能量图中的能量来填充地图的第一行。
for (let x = 0; x < w; x += 1) {
const y = 0;
seamsEnergies[y][x] = {
energy: energyMap[y][x],
coordinate: { x, y },
previous: null,
};
}
// 填充其余行。
for (let y = 1; y < h; y += 1) {
for (let x = 0; x < w; x += 1) {
// 查找具有最小能量的上方相邻单元格。
// 这个单元格将是此时具有最低能量的缝的尾部。
// 这并不意味着这条缝(路径)在全球范围内具有最低能量。
// 相反,这意味着我们已经找到了一个具有最低能量的路径,这可能会引导我们到达当前坐标为 x 和 y 的像素。
let minPrevEnergy = Infinity;
let minPrevX: number = x;
for (let i = (x - 1); i <= (x + 1); i += 1) {
if (i >= 0 && i < w && seamsEnergies[y - 1][i].energy < minPrevEnergy) {
minPrevEnergy = seamsEnergies[y - 1][i].energy;
minPrevX = i;
}
}
// 更新当前单元格。
seamsEnergies[y][x] = {
energy: minPrevEnergy + energyMap[y][x],
coordinate: { x, y },
previous: { x: minPrevX, y: y - 1 },
};
}
}
// 查找最低能量缝的结束位置。
// 我们需要找到最低能量缝的尾部以开始从尾部到头部的遍历(从下到上)。
let lastMinCoordinate: Coordinate | null = null;
let minSeamEnergy = Infinity;
for (let x = 0; x < w; x += 1) {
const y = h - 1;
if (seamsEnergies[y][x].energy < minSeamEnergy) {
minSeamEnergy = seamsEnergies[y][x].energy;
lastMinCoordinate = { x, y };
}
}
// 查找最低能量缝。
// 一旦我们知道尾部在哪里,我们就可以根据缝像素元数据的“previous”值遍历并组装最低能量缝。
const seam: Seam = [];
if (!lastMinCoordinate) {
return seam;
}
const { x: lastMinX, y: lastMinY } = lastMinCoordinate;
// 逐个向缝路径添加新像素,直到我们到达顶部。
let currentSeam = seamsEnergies[lastMinY][lastMinX];
while (currentSeam) {
seam.push(currentSeam.coordinate);
const prevMinCoordinates = currentSeam.previous;
if (!prevMinCoordinates) {
currentSeam = null;
} else {
const { x: prevMinX, y: prevMinY } = prevMinCoordinates;
currentSeam = seamsEnergies[prevMinY][prevMinX];
}
}
return seam;
};
移除最低能量的缝
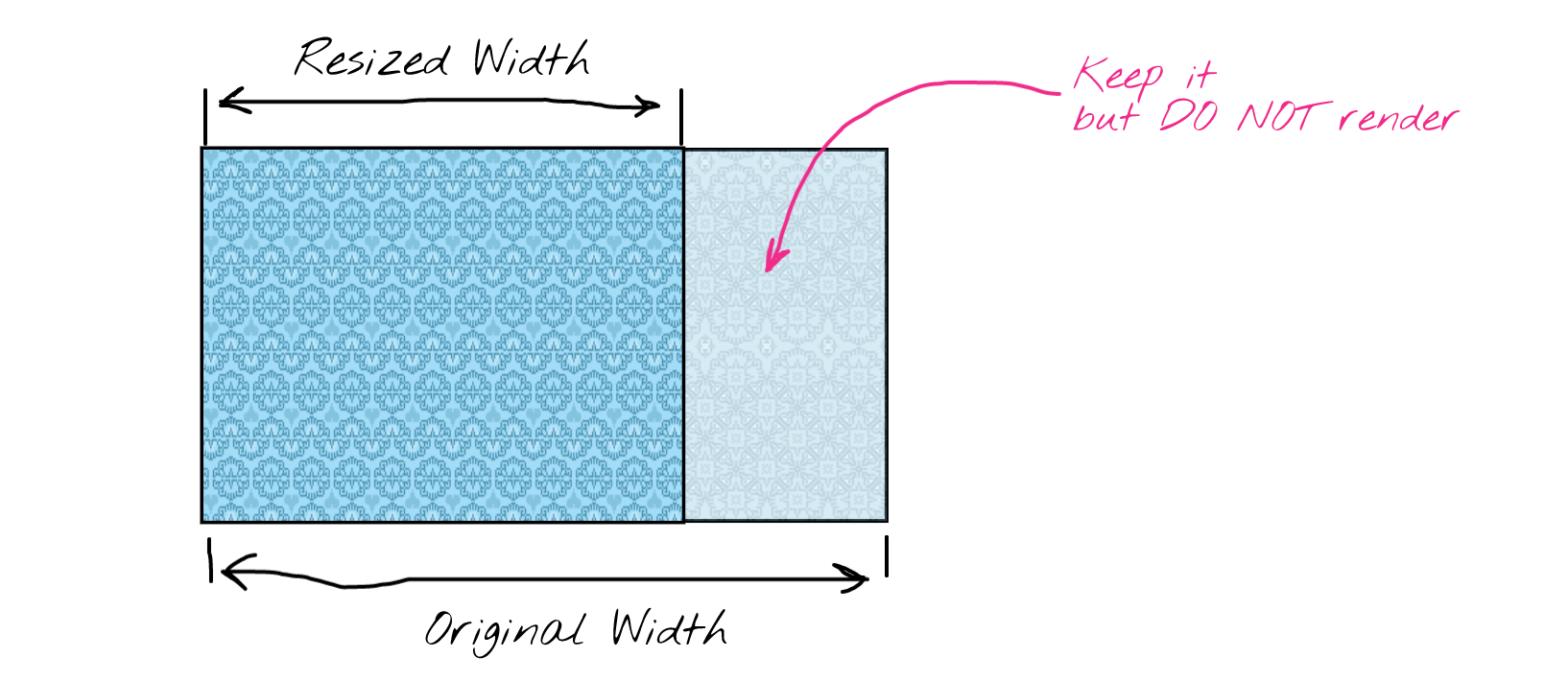
一旦我们找到了最低能量的缝,我们就需要从图像中移除(雕刻)构成它的像素。移除是通过将缝右侧的像素向左移动 1px 来实现的。出于性能原因,我们实际上不会删除最后几列。相反,渲染组件将只忽略超出调整后图像宽度的图像部分。
// 从图像数据中删除缝。
// 我们在每一行中删除像素,然后将剩余的行像素向左移动。
const deleteSeam = (img: ImageData, seam: Seam, { w }: ImageSize): void => {
seam.forEach(({ x: seamX, y: seamY }: Coordinate) => {
for (let x = seamX; x < (w - 1); x += 1) {
const nextPixel = getPixel(img, { x: x + 1, y: seamY });
setPixel(img, { x, y: seamY }, nextPixel);
}
});
};
对象移除
缝切割算法首先尝试移除由低能量像素组成的缝。我们可以利用这一事实,通过手动为某些像素分配低能量(即通过在图像上绘制并遮盖某些区域),使缝切割算法为我们免费执行对象移除。
目前,在getPixelEnergy()函数中,我们仅使用R、G、B颜色通道来计算像素的能量。但是,我们还没有使用颜色的A(透明度)参数。我们可以使用透明度通道告诉算法,透明像素是我们想要移除的像素。您可以查看能量函数的源代码,了解它如何考虑透明度。
这里是对象移除算法的工作原理。

存在的问题和下一步计划
当然,JS IMAGE CARVER网络应用程序还远未成为一个生产就绪的调整器。其主要目的是交互式地实验性地使用Seam Carving算法。因此,未来的计划是继续进行实验。
原始论文描述了Seam Carving算法不仅可用于缩小图像,还可以用于放大图像。反过来,放大可能用于在移除对象后,将图像放大回其原始宽度。
另一个有趣的实验领域可能是使算法在实时中工作。
这是未来的计划,但目前,我希望关于图像缩小的示例对您来说既有趣又有用。我还希望您已经了解到使用动态规划来实现它的想法。
所以,祝您自己的实验好运!