LRU 캐시 알고리즘

LRU 캐시 알고리즘 은 사용된 순서대로 아이템을 정리함으로써, 오랜 시간 동안 사용되지 않은 아이템을 빠르게 찾아낼 수 있도록 한다.

한방향으로만 옷을 걸 수 있는 옷걸이 행거를 생각해봅시다. 가장 오랫동안 입지 않은 옷을 찾기 위해서는, 행거의 반대쪽 끝을 보면 됩니다.

문제 정의

LRUCache 클래스를 구현해봅시다:

LRUCache(int capacity) LRU 캐시를 양수 의 capacity 로 초기화합니다.
int get(int key) key 가 존재할 경우 key 값을 반환하고, 그렇지 않으면 undefined 를 반환합니다.
void set(int key, int value) key 가 존재할 경우 key 값을 업데이트 하고, 그렇지 않으면 key-value 쌍을 캐시에 추가합니다. 만약 이 동작으로 인해 키 개수가 capacity 를 넘는 경우, 가장 오래된 키 값을 제거 합니다.

get() 과 set() 함수는 무조건 평균 O(1) 의 시간 복잡도 내에 실행되어야 합니다.

구현

버전 1: 더블 링크드 리스트 + 해시맵

LRUCache.js 에서 LRUCache 구현체 예시를 확인할 수 있습니다. 예시에서는 (평균적으로) 빠른 O(1) 캐시 아이템 접근을 위해 HashMap 을 사용했고, (평균적으로) 빠른 O(1) 캐시 아이템 수정과 제거를 위해 DoublyLinkedList 를 사용했습니다. (허용된 최대의 캐시 용량을 유지하기 위해)

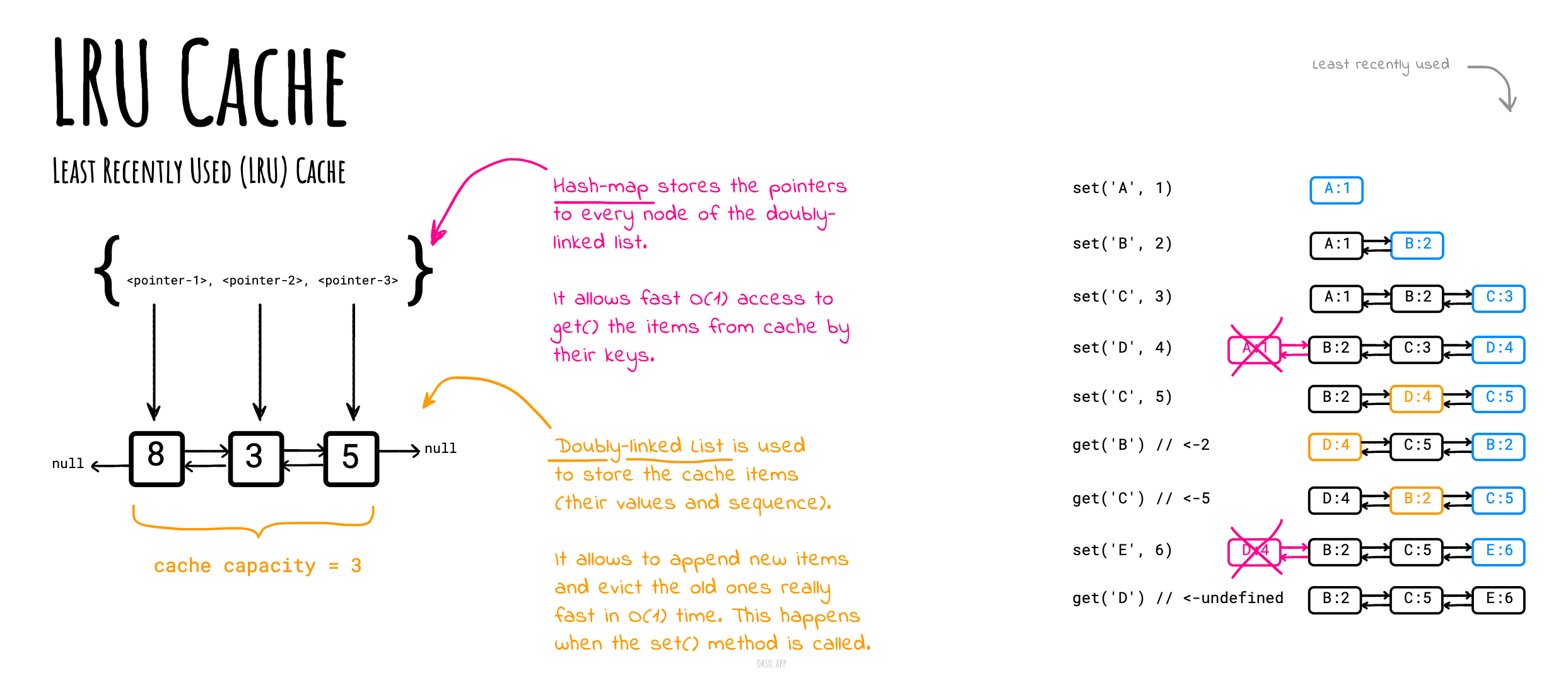
Linked List

okso.app 으로 만듦

LRU 캐시가 어떻게 작동하는지 더 많은 예시로 확인하고 싶다면 LRUCache.test.js](./test/LRUCache.test.js) 파일을 참고하세요.

버전 2: 정렬된 맵

더블 링크드 리스트로 구현한 첫번째 예시는 어떻게 평균 O(1) 시간 복잡도가 set() 과 get() 으로 나올 수 있는지 학습 목적과 이해를 돕기 위해 좋은 예시입니다.

그러나, 더 쉬운 방법은 자바스크립트의 Map 객체를 사용하는 것입니다. 이 Map 객체는 키-값 쌍과 키를 추가하는 순서 원본 을 지닙니다. 우리는 이걸 아이템을 제거하거나 다시 추가하면서 맵의 "가장 마지막" 동작에서 최근에 사용된 아이템을 유지하기 위해 사용할 수 있습니다. Map 의 시작점에 있는 아이템은 캐시 용량이 넘칠 경우 가장 먼저 제거되는 대상입니다. 아이템의 순서는 map.keys() 와 같은 IterableIterator 을 사용해 확인할 수 있습니다.

해당 구현체는 LRUCacheOnMap.js 의 LRUCacheOnMap 예시에서 확인할 수 있습니다.

이 LRU 캐시 방식이 어떻게 작동하는지 더 많은 테스트 케이스를 확인하고 싶다면 LRUCacheOnMap.test.js 파일을 참고하세요.

복잡도

	평균
공간	`O(n)`
아이템 찾기	`O(1)`
아이템 설정하기	`O(1)`

LRU 캐시 알고리즘

문제 정의

구현

버전 1: 더블 링크드 리스트 + 해시맵

버전 2: 정렬된 맵

복잡도

참조