GPT4All Python SDK
安装
要开始使用,请将gpt4all包安装到您的python环境中。
我们建议使用gpt4all将其安装到自己的虚拟环境中使用venv或conda
加载LLM
模型通过名称通过GPT4All类加载。如果您是第一次加载模型,它将被下载到您的设备并保存,以便下次创建具有相同名称的GPT4All模型时可以快速重新加载。
加载LLM
GPT4All模型名称 |
文件大小 | 所需RAM | 参数 | 量化 | 开发者 | 许可证 | MD5总和(唯一哈希) |
|---|---|---|---|---|---|---|---|
Meta-Llama-3-8B-Instruct.Q4_0.gguf |
4.66 GB | 8 GB | 80亿 | q4_0 | Meta | Llama 3许可证 | c87ad09e1e4c8f9c35a5fcef52b6f1c9 |
Nous-Hermes-2-Mistral-7B-DPO.Q4_0.gguf |
4.11 GB | 8 GB | 70亿 | q4_0 | Mistral & Nous Research | Apache 2.0 | Coa5f6b4eabd3992da4d7fb7f020f921eb |
Phi-3-mini-4k-instruct.Q4_0.gguf |
2.18 GB | 4 GB | 38亿 | q4_0 | Microsoft | MIT | f8347badde9bfc2efbe89124d78ddaf5 |
orca-mini-3b-gguf2-q4_0.gguf |
1.98 GB | 4 GB | 30亿 | q4_0 | Microsoft | CC-BY-NC-SA-4.0 | 0e769317b90ac30d6e09486d61fefa26 |
gpt4all-13b-snoozy-q4_0.gguf |
7.37 GB | 16 GB | 130亿 | q4_0 | Nomic AI | GPL | 40388eb2f8d16bb5d08c96fdfaac6b2c |
聊天会话生成
您将从HuggingFace访问的大多数语言模型都已被训练为助手。这指导语言模型不仅用相关的文本回答,而且有帮助的文本。
如果您希望您的LLM的回复在通常意义上是有帮助的,我们建议您应用模型微调时使用的聊天模板。特定提示模板的信息通常可以在模型的官方HuggingFace页面上找到。
示例LLM聊天会话生成
加载Llama 3并在聊天会话中输入以下提示:
使用默认的采样设置,您应该看到类似以下内容:
The quadratic formula!
The quadratic formula is a mathematical formula that provides the solutions to a quadratic equation of the form:
ax^2 + bx + c = 0
where a, b, and c are constants. The formula is:
x = (-b ± √(b^2 - 4ac)) / 2a
Let's break it down:
* x is the variable we're trying to solve for.
* a, b, and c are the coefficients of the quadratic equation.
* ± means "plus or minus".
* √ denotes the square root.
To use the formula, simply plug in the values of a, b, and c into the expression above. The resulting value(s) will be the solutions to the original quadratic equation!
For example, let's say we have the quadratic equation:
x^2 + 5x + 6 = 0
We can plug these values into the formula as follows:
a = 1
b = 5
直接生成
直接调用model.generate()提示模型而不应用任何模板。
注意:这可能导致回复不像有帮助的回复,更像镜像您的提示的语气。通常,在聊天会话之外的语言模型更像是一个透镜,而不是一个助手,它揭示了模型训练数据的分布。
例如,看看当我们将上述相同提示提供给模型而不应用聊天会话时,模型的回复如何变化:
示例LLM直接生成
加载Llama 3并输入以下提示:
使用默认的采样设置,您应该看到类似以下内容:
. The equation is in the form of a + bx = c, where a and b are constants.
The solution to this problem involves using the quadratic formula which states that for any quadratic equation ax^2+bx+c=0, its solutions can be found by:
x = (-b ± √(b^2-4ac)) / 2a
In your case, since you have a + bx = c, we need to rewrite it in the form of ax^2+bx+c=0. To do this, subtract both sides from c, so that:
c - (a + bx) = 0
Now, combine like terms on the left side and simplify:
ax^2 + (-b)x + (c-a) = 0\n\nSo now we have a quadratic equation in standard form: ax^2+bx+c=0. We can use this to find its solutions using the quadratic formula:
x = ((-b ± √((-b)^2
为什么它有不同的回复?因为语言模型在被微调为助手之前,被训练得更像数据模仿而不是有帮助的助手。因此,我们的回复最终更像数学风格的文本的典型延续,而不是对话中的有帮助的答案。
嵌入式
Nomic培训和开源免费的嵌入式模型,这些模型在您的硬件上运行非常快。
在本地运行文本嵌入式模型的最简单方法使用nomicpython库来接口我们的快速C/C++实现.
示例嵌入式生成
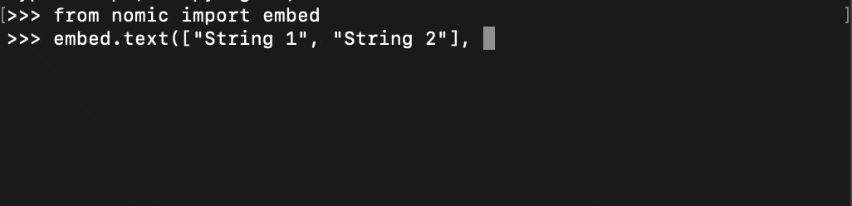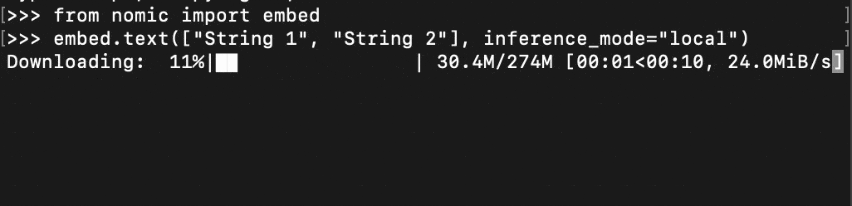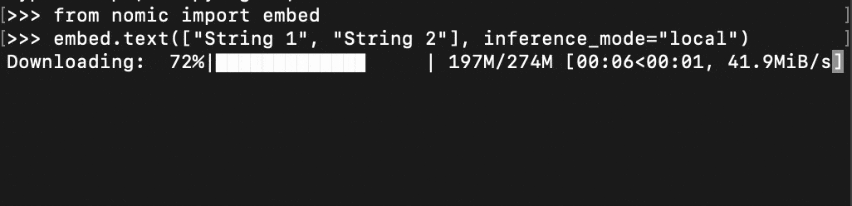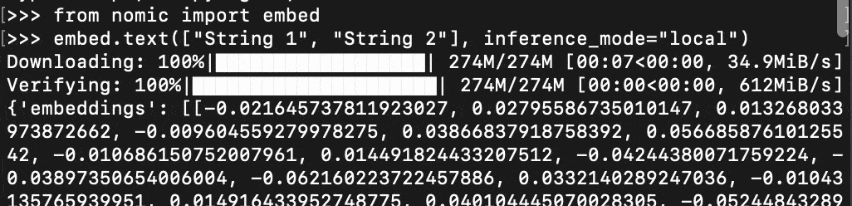
从embed库导入nomic,您可以调用embed.text()使用inference_mode="local"。这下载了一个嵌入式模型并保存以供以后使用。
要了解更多关于使用nomic在本地制作嵌入的信息,请访问我们的嵌入指南.
以下嵌入式模型可以在应用程序中使用,并使用来自Embed4All库的gpt4all类。GGUF文件的默认上下文长度为2048,但可以扩展.
| 名称 | 使用nomic |
Embed4All模型名称 |
上下文长度 | # 嵌入维度 | 文件大小 |
|---|---|---|---|---|---|
| Nomic嵌入式v1 | embed.text(strings, model="nomic-embed-text-v1", inference_mode="local") |
Embed4All("nomic-embed-text-v1.f16.gguf") |
2048 | 768 | 262 MiB |
| Nomic嵌入式v1.5 | embed.text(strings, model="nomic-embed-text-v1.5", inference_mode="local") |
Embed4All("nomic-embed-text-v1.5.f16.gguf") |
2048 | 64-768 | 262 MiB |
| SBert | 无 | Embed4All("all-MiniLM-L6-v2.gguf2.f16.gguf") |
512 | 384 | 44 MiB |