投资组合策略：投资组合管理

简介

投资组合策略 旨在支持多种投资组合策略，这意味着用户可以根据 预测模型 的预测得分，采用不同算法生成投资组合。用户可通过 投资组合策略 结合 工作流 模块实现自动化流程，详情请参阅工作流：工作流管理。

由于 Qlib 中的组件采用松耦合设计，投资组合策略 也可作为独立模块使用。

Qlib 提供了多种已实现的投资组合策略，同时也支持自定义策略，用户可根据自身需求定制策略。

用户在指定模型（预测信号）和策略后，运行回测可帮助其评估自定义模型（预测信号）/策略的性能。

基类与接口

BaseStrategy

Qlib 提供了一个基类 qlib.strategy.base.BaseStrategy。所有策略类均需继承该基类并实现其接口。

generate_trade_decision
generate_trade_decision 是一个关键接口，用于在每个交易时段生成交易决策。该方法的调用频率取决于执行器的频率（默认为 “time_per_step”=”day”），但具体的交易频率可由用户自行实现决定。例如，若用户希望以周为单位交易，而执行器的 time_per_step 设置为 “day”，则用户可每周返回非空的 TradeDecision（否则返回空值，如此例所示）。

用户可继承 BaseStrategy 来自定义其策略类。

WeightStrategyBase

Qlib 还提供了一个类 qlib.contrib.strategy.WeightStrategyBase，它是 BaseStrategy 的子类。

WeightStrategyBase 仅关注目标持仓，并根据持仓自动生成订单列表。它提供了 generate_target_weight_position 接口。

generate_target_weight_position
- 根据当前持仓和交易日期生成目标持仓。输出的权重分布不考虑现金。
- 返回目标持仓。
注意

此处的目标持仓指目标资产占总资产的百分比。

WeightStrategyBase 实现了 generate_order_list 接口，其处理流程如下。

调用 generate_target_weight_position 方法生成目标持仓。
根据目标持仓生成目标股票数量。
根据目标股票数量生成订单列表。

用户可以继承 WeightStrategyBase 并实现接口 generate_target_weight_position，以自定义仅关注目标持仓的策略类。

已实现的策略

Qlib 提供了一个名为 TopkDropoutStrategy 的已实现策略类。

TopkDropoutStrategy

TopkDropoutStrategy 是 BaseStrategy 的子类，并实现了接口 generate_order_list，其处理流程如下。

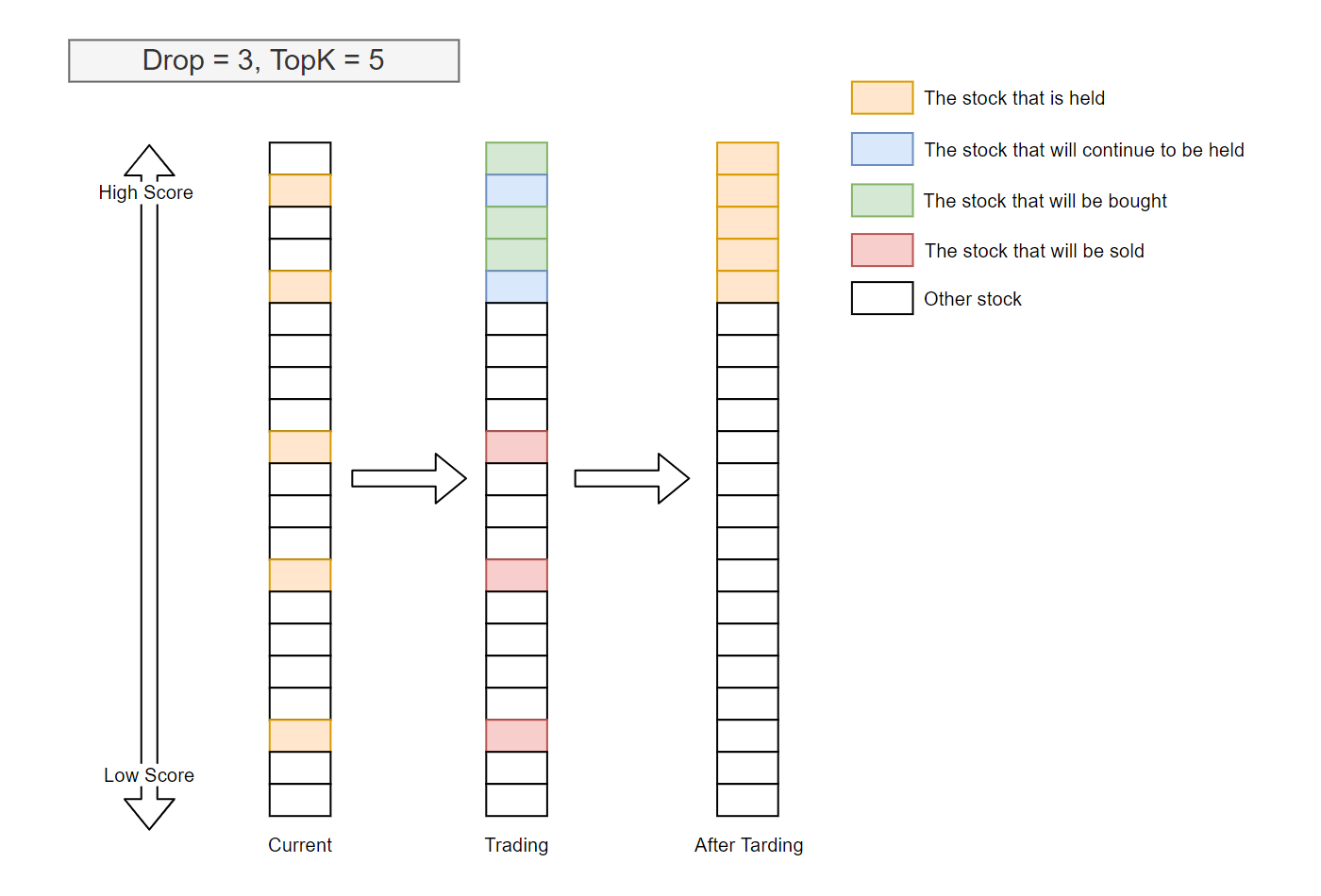
采用 Topk-Drop 算法计算每只股票的目标数量。
注意

Topk-Drop 算法有两个参数：
- Topk：持有的股票数量。
- Drop：每个交易日卖出的股票数量。
通常情况下，当前持有的股票数量为 Topk，但在交易初期可能为零。对于每个交易日，设 $d$ 为当前持有且按预测得分从高到低排序后排名大于 $K$ 的证券数量。然后，将卖出当前持有的 $d$ 只得分最差的股票，并买入相同数量的未持有但预测得分最高的股票。

通常情况下，$d=$`Drop`，尤其当候选证券池较大、$K$ 较大且 Drop 较小时。

在大多数情况下，TopkDrop 算法每个交易日卖出和买入 Drop 只股票，从而产生 $2\times$`Drop`/$K$ 的换手率。

下图展示了一个典型场景。
根据目标股票数量生成订单列表。

EnhancedIndexingStrategy

EnhancedIndexingStrategy 增强型指数化策略结合了主动管理与被动管理的精髓，旨在在控制风险暴露（即跟踪误差）的同时，实现超越基准指数（如标普 500）的投资组合收益。

更多信息请参阅 qlib.contrib.strategy.signal_strategy.EnhancedIndexingStrategy 和 qlib.contrib.strategy.optimizer.enhanced_indexing.EnhancedIndexingOptimizer。

用法与示例

首先，用户可以创建一个模型以获取交易信号（以下示例中变量名为 pred_score）。

预测得分

预测得分是一个 pandas DataFrame，其索引为，且必须包含一个 score 列。

一个预测样本如下所示。

  datetime instrument     score
2019-01-04   SH600000 -0.505488
2019-01-04   SZ002531 -0.320391
2019-01-04   SZ000999  0.583808
2019-01-04   SZ300569  0.819628
2019-01-04   SZ001696 -0.137140
             ...            ...
2019-04-30   SZ000996 -1.027618
2019-04-30   SH603127  0.225677
2019-04-30   SH603126  0.462443
2019-04-30   SH603133 -0.302460
2019-04-30   SZ300760 -0.126383

Forecast Model 模块可进行预测，请参阅预测模型：模型训练与预测。

通常，预测得分是模型的输出。但某些模型是从具有不同量纲的标签中学习的，因此预测得分的量纲可能与您的预期不同（例如，证券的收益率）。

Qlib 没有添加将预测分数缩放到统一尺度的步骤，原因如下：- 并非每种交易策略都关心分数的尺度（例如，TopkDropoutStrategy 仅关心排序）。因此，策略本身负责重新缩放预测分数（例如，一些基于投资组合优化的策略可能需要有意义的尺度）。- 模型具有灵活性，可以自定义目标、损失函数和数据处理方式。因此，我们不认为仅根据模型输出就能直接找到一种通用方法将其重新缩放回来。如果你希望将其缩放回某些有意义的值（例如股票收益），一个直观的解决方案是为模型的近期输出和你的近期目标值构建一个回归模型。

运行回测

在大多数情况下，用户可以使用 backtest_daily 对其投资组合管理策略进行回测。

from pprint import pprint

import qlib
import pandas as pd
from qlib.utils.time import Freq
from qlib.utils import flatten_dict
from qlib.contrib.evaluate import backtest_daily
from qlib.contrib.evaluate import risk_analysis
from qlib.contrib.strategy import TopkDropoutStrategy

# init qlib
qlib.init(provider_uri=<qlib data dir>)

CSI300_BENCH = "SH000300"
STRATEGY_CONFIG = {
    "topk": 50,
    "n_drop": 5,
    # pred_score, pd.Series
    "signal": pred_score,
}


strategy_obj = TopkDropoutStrategy(**STRATEGY_CONFIG)
report_normal, positions_normal = backtest_daily(
    start_time="2017-01-01", end_time="2020-08-01", strategy=strategy_obj
)
analysis = dict()
# default frequency will be daily (i.e. "day")
analysis["excess_return_without_cost"] = risk_analysis(report_normal["return"] - report_normal["bench"])
analysis["excess_return_with_cost"] = risk_analysis(report_normal["return"] - report_normal["bench"] - report_normal["cost"])

analysis_df = pd.concat(analysis)  # type: pd.DataFrame
pprint(analysis_df)

如果用户希望更细致地控制其策略（例如，用户拥有更高级的执行器版本），可以参考以下示例。

from pprint import pprint

import qlib
import pandas as pd
from qlib.utils.time import Freq
from qlib.utils import flatten_dict
from qlib.backtest import backtest, executor
from qlib.contrib.evaluate import risk_analysis
from qlib.contrib.strategy import TopkDropoutStrategy

# init qlib
qlib.init(provider_uri=<qlib data dir>)

CSI300_BENCH = "SH000300"
# Benchmark is for calculating the excess return of your strategy.
# Its data format will be like **ONE normal instrument**.
# For example, you can query its data with the code below
# `D.features(["SH000300"], ["$close"], start_time='2010-01-01', end_time='2017-12-31', freq='day')`
# It is different from the argument `market`, which indicates a universe of stocks (e.g. **A SET** of stocks like csi300)
# For example, you can query all data from a stock market with the code below.
# ` D.features(D.instruments(market='csi300'), ["$close"], start_time='2010-01-01', end_time='2017-12-31', freq='day')`

FREQ = "day"
STRATEGY_CONFIG = {
    "topk": 50,
    "n_drop": 5,
    # pred_score, pd.Series
    "signal": pred_score,
}

EXECUTOR_CONFIG = {
    "time_per_step": "day",
    "generate_portfolio_metrics": True,
}

backtest_config = {
    "start_time": "2017-01-01",
    "end_time": "2020-08-01",
    "account": 100000000,
    "benchmark": CSI300_BENCH,
    "exchange_kwargs": {
        "freq": FREQ,
        "limit_threshold": 0.095,
        "deal_price": "close",
        "open_cost": 0.0005,
        "close_cost": 0.0015,
        "min_cost": 5,
    },
}

# strategy object
strategy_obj = TopkDropoutStrategy(**STRATEGY_CONFIG)
# executor object
executor_obj = executor.SimulatorExecutor(**EXECUTOR_CONFIG)
# backtest
portfolio_metric_dict, indicator_dict = backtest(executor=executor_obj, strategy=strategy_obj, **backtest_config)
analysis_freq = "{0}{1}".format(*Freq.parse(FREQ))
# backtest info
report_normal, positions_normal = portfolio_metric_dict.get(analysis_freq)

# analysis
analysis = dict()
analysis["excess_return_without_cost"] = risk_analysis(
    report_normal["return"] - report_normal["bench"], freq=analysis_freq
)
analysis["excess_return_with_cost"] = risk_analysis(
    report_normal["return"] - report_normal["bench"] - report_normal["cost"], freq=analysis_freq
)

analysis_df = pd.concat(analysis)  # type: pd.DataFrame
# log metrics
analysis_dict = flatten_dict(analysis_df["risk"].unstack().T.to_dict())
# print out results
pprint(f"The following are analysis results of benchmark return({analysis_freq}).")
pprint(risk_analysis(report_normal["bench"], freq=analysis_freq))
pprint(f"The following are analysis results of the excess return without cost({analysis_freq}).")
pprint(analysis["excess_return_without_cost"])
pprint(f"The following are analysis results of the excess return with cost({analysis_freq}).")
pprint(analysis["excess_return_with_cost"])

结果

回测结果如下所示：

                                                  risk
excess_return_without_cost mean               0.000605
                           std                0.005481
                           annualized_return  0.152373
                           information_ratio  1.751319
                           max_drawdown      -0.059055
excess_return_with_cost    mean               0.000410
                           std                0.005478
                           annualized_return  0.103265
                           information_ratio  1.187411
                           max_drawdown      -0.075024

无成本超额收益
- 均值
  无交易成本的 CAR（累计异常收益）的均值
- std
  无成本累积异常收益（CAR）的标准差。
- 年化收益
  无成本累积异常收益（CAR）的年化收益率。
- 信息比率
  无交易成本的信息比率。请参阅信息比率 – IR。
- 最大回撤
  无交易成本的 CAR（累计异常收益）的最大回撤，请参阅最大回撤（MDD）。
有成本超额收益
- 均值
  有交易成本的 CAR（累计异常收益）序列的均值
- std
  有交易成本的 CAR（累计异常收益）序列的标准差。
- 年化收益
  有成本累积异常收益（CAR）的年化收益率。
- 信息比率
  有交易成本的信息比率。请参阅信息比率 – IR。
- 最大回撤
  有交易成本的 CAR（累计异常收益）的最大回撤，请参阅最大回撤（MDD）。

参考

有关 Forecast Model 输出的预测分数 pred_score 的更多信息，请参阅预测模型：模型训练与预测。